Trigonométrie
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
etretat
- Membre Naturel
- Messages: 18
- Enregistré le: 16 Avr 2009, 19:31
-
 par etretat » 16 Avr 2009, 19:37
par etretat » 16 Avr 2009, 19:37
Bonjour , j'ai besoin de votre aide car je n'arrive pas à finir de résoudre cette équation.
F est la fonction définie par R par f(x)=sin(2x+/3)-1
f'(x)=2cos(2x+/3)
Résoudre f'(x)=0
Alors j'ai fait : f'(x)=0 : résolution dans IR
2cos(2x+pi/3)=0
cos(2x+pi/3)=0
cos(2x+pi/3)=cos pi/2
2x+pi/3=pi/2 +2kpi ou 2x+pi/3=-pi/2 +2kpi
2x=pi/2 -pi/3+2kpi ou 2x=-pi/2-pi/3 +2kpi
x=pi/4 -pi/6+kpi ou x=-pi/4-pi/6 +kpi
x=pi/12+kpi ou x=-5pi/12+kpi
En remarquant que (avec k=1) -5pi/12+=pi/12, on a donc f '(x)=0 x=pi/12+kpi
2)déterminer le signe de f'(x) dans l'intervalle (0,pi)
Merci pour votre aide.
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 16 Avr 2009, 20:29
par uztop » 16 Avr 2009, 20:29
Bonjour,
il y a un petit problème à la fin de ta résolution de f'(x)= 0

avec k=1, ça fait
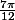
, et pas
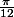
; l'équation a donc bien deux solutions dans l'intervalle
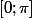
-
etretat
- Membre Naturel
- Messages: 18
- Enregistré le: 16 Avr 2009, 19:31
-
 par etretat » 16 Avr 2009, 20:34
par etretat » 16 Avr 2009, 20:34
Merci pour ta réponse mais pourrais tu expliciter pourquoi y a t-il 2 solution?
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 16 Avr 2009, 20:43
par uztop » 16 Avr 2009, 20:43
tu as trouvé deux solutions avec tes calculs:
x=pi/12+kpi ou x=-5pi/12+kpi
Après, tu as dit que les deux solutions sont en fait égales, ce qui est faux, c'est tout. Dans tout ce que tu as écrit, il n'y a que la dernière ligne qui est fausse.
-
etretat
- Membre Naturel
- Messages: 18
- Enregistré le: 16 Avr 2009, 19:31
-
 par etretat » 16 Avr 2009, 20:57
par etretat » 16 Avr 2009, 20:57
Ok donc les solutions sont -7pi/12 et pi/12 c sa ?
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 16 Avr 2009, 21:15
par uztop » 16 Avr 2009, 21:15
non, c'est pi/12 et 7pi/12 (pas de -)
-
etretat
- Membre Naturel
- Messages: 18
- Enregistré le: 16 Avr 2009, 19:31
-
 par etretat » 16 Avr 2009, 21:23
par etretat » 16 Avr 2009, 21:23
Merci beaucoup , mais j'ai encore besoin de ton aide pour pouvoir déterminer le signe de f'(x) entre (0,pi). Je n'arrive pas à comprendre . Merci
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 16 Avr 2009, 21:27
par uztop » 16 Avr 2009, 21:27
pour x < pi/12, quel est le signe de f'(x) ? tu peux essayer x=0 par exemple
pour x entre pi/12 et 7pi/12 ? là aussi choisis un x qui te plait ?
pour le dernier intervalle, tu peux choisir x=pi par exemple.
Il suffit de choisir une valeur de x dans chaque intervalle parce que tu sais que f' ne change pas de signe à l'intérieur de ces intervalles.
-
etretat
- Membre Naturel
- Messages: 18
- Enregistré le: 16 Avr 2009, 19:31
-
 par etretat » 16 Avr 2009, 21:35
par etretat » 16 Avr 2009, 21:35
Je ne comprends pas 'dans chaque intervalle".Comment on peut choisir x?
-
etretat
- Membre Naturel
- Messages: 18
- Enregistré le: 16 Avr 2009, 19:31
-
 par etretat » 16 Avr 2009, 21:38
par etretat » 16 Avr 2009, 21:38
A si j'ai bien compris le 1 intervalle x>7pi/12 ou x>pi/12
2 " " " 7pi/12>x>pi/12
3 " " " " " " x<7pi/12 ou x
C sa?
-
etretat
- Membre Naturel
- Messages: 18
- Enregistré le: 16 Avr 2009, 19:31
-
 par etretat » 16 Avr 2009, 21:44
par etretat » 16 Avr 2009, 21:44
La question c'est de déterminer le signe de f' dans l'intervalle (0,pi) , ce n'est pas avec un tableau de signes et les valeurs qui annulent la dérivée???
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 16 Avr 2009, 21:46
par uztop » 16 Avr 2009, 21:46
dans [0, pi], les trois intervalles à considérer sont:
[0, pi/12] ; [pi/12, 7pi/12] et [7pi/12, pi]
La dérivée s'annule en pi/12 et 7pi/12 comme on l'a vu.
-
etretat
- Membre Naturel
- Messages: 18
- Enregistré le: 16 Avr 2009, 19:31
-
 par etretat » 16 Avr 2009, 21:49
par etretat » 16 Avr 2009, 21:49
ok donc ensuite on fait comment? (un tableau?)
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 16 Avr 2009, 21:49
par uztop » 16 Avr 2009, 21:49
oui, avec ça tu as tout ce qu'il faut pour faire un tableau de signes
-
etretat
- Membre Naturel
- Messages: 18
- Enregistré le: 16 Avr 2009, 19:31
-
 par etretat » 16 Avr 2009, 21:51
par etretat » 16 Avr 2009, 21:51
Mais comment fait-on pour remplir le tableau de signes car je sais le faire avec une fonction polynome mais avec la trigo.
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 16 Avr 2009, 21:52
par uztop » 16 Avr 2009, 21:52
c'est ce que je disais tout à l'heure, la fonction ne change pas de signe à l'intérieur des intervalles. Il suffit donc de choisir une valeur de x dans chacun des intervalles pour déterminer le signe.
-
etretat
- Membre Naturel
- Messages: 18
- Enregistré le: 16 Avr 2009, 19:31
-
 par etretat » 16 Avr 2009, 21:57
par etretat » 16 Avr 2009, 21:57
En fait faut choisir n'importe quel x dans les 3 intervalles et remplacer ce x dans f'(x) et si c'est négatif on mais un signe - et ainsi de suite. (mais comment choisis le x approprié ?)
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 16 Avr 2009, 22:03
par uztop » 16 Avr 2009, 22:03
comme tu veux pourvu qu'il soit bien dans l'intervalle. Donc autant prendre des valeurs qui simplifient les calculs; pour le premier intervalle x=0 est très bien par exemple.
-
etretat
- Membre Naturel
- Messages: 18
- Enregistré le: 16 Avr 2009, 19:31
-
 par etretat » 16 Avr 2009, 22:05
par etretat » 16 Avr 2009, 22:05
Ok , donc pour le 2 intervalle je peux prendre pi/12 et pour le 3ème pi?
Et si les solutions de ses 3 calculs sont de signes négatifs donc je mets un signe - dans l'intervalle concernés c sa ?
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 16 Avr 2009, 22:07
par uztop » 16 Avr 2009, 22:07
pour le troisième, tu peux prendre pi oui. Pour le deuxième pi/12 n'est pas une très bonne idée puisque tu vas trouver 0, ce qui ne te renseigne pas sur le signe. Tu peux prendre pi/2 par exemple qui donne des calculs tout simples.
Et si les solutions de ses 3 calculs sont de signes négatifs donc je mets un signe - dans l'intervalle concernés c sa ?
oui, mais tu ne vas pas trouver des - partout

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités

