Égalité à démontrer (trigonométrie)

[vDJ]

Bonjour, je suis nouveau sur ce forum.
J'ai besoin d'aide quant à un exercice au cours duquel je dois montrer que = 2*cos
(On est en radians bien sûr)
(Désolé si TEX n'est pas bien utilisé, je viens de découvrir)

Seulement, je ne vois pas du tout comment faire...Quelqu'un a une idée ?
Merci d'avance !

[uztop]

Bonjour et bienvenu sur le forum !

ton énoncé ne contient que ça ? Il n'y a aucune indication ?
En fait, ton exercice revient à vouloir calculer ou
Ce n'est pas un exercice très difficile, mais c'est pas évident sans indications. Au fait, tu es en terminale ?

[vDJ]

Merci de ta réponse rapide.
Non, l'exercice ne contient pas uniquement cette question : j'ai juste indiqué l'endroit où je suis bloqué.
Par ailleurs, je suis en 1ère. Est-ce que c'est d'un niveau trop élevé pour moi, ce qui indiquerait que je me suis trompé avant ?

[aeon]

Il faudrait avoir l'énoncé complet auparavant.

[uztop]

Est-ce que c'est d'un niveau trop élevé pour moi, ce qui indiquerait que je me suis trompé avant ?

non, ça dire que tu t'es trompé avant; d'ailleurs l'égalité que tu veux prouver est vraie. Je te demandais ta classe pour ne pas t'embrouiller avec des indications que tu risques de ne pas comprendre.
Sinon, comme dit aeon, tu devrais donner l'énoncé complet

[vDJ]

Bon, je me sens pas de recopier tout l'énoncé...
J'ai fait un screenshot de la figure, sous GeoGebra :
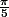
Le triangle AOB est isocèle : AB = 1 (ne pas se fier à la figure, j'ai pris une unité arbitraire), l'angle AOB = (ne pas se fier non plus au 36,04º et autres, c'est le logiciel qui calcule ça)
On doit montrer que AO = 2*cos
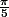
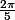
Le seul moyen que j'ai trouvé de calculer AO est de creer un triangle AOM, avec M milieu de AB (donc AM = 0.5), puis trigonométrie, vu que MAO = , alors AO = .

Désolé si la figure n'est pas très claire ! (Et puis elle est un peu grande, désolé pour les petites résolutions d'écran)

PS: La droite qui coupe l'angle A est sa bissectrice, elle coupe OB en J. L est le projeté orthogonal de J sur AO, et K celui sur AB.
PS2:J'oubliais, L est le milieu de AO
Merci !

[uztop]

ok merci pour la figure qui est tres claire.
Concernant le PS2, est ce que c'est quelque chose que tu as demontre precedemment ? Dans ce cas, il faut l'utiliser. (OA = 2 LA)
Voici quelques indications pour ton exo:
- quelle est la valeur de l'angle LAJ ?
- que peut-on dire du triangle LAJ ?
Tu vas aussi avoir besoin de AJ, pour cela, que peux-tu dire tu triangle AJB ?
J'espere que ca va t'aider; je vais me reconnecter ce soir (je suis au travail maintenant et je ne peux pas trop me connecter pendant le journee)

[vDJ]

AH ! JE SUIS TROP NIAIS !
Damned, c'est évident !
Oui, le PS2, je l'ai démontré précedemment.
On a AJ = AB = 1 (car AJB isocèle)
donc, comme LAJ rectangle, on peut dire que LA = 1*cos (pi/5)
Donc, puisque AB = 2LA, AB = 2*cos (pi/5) !
Je l'avais vraiment sous le nez...
J'ai des doutes quant à mes capacités, des fois :triste:
Merci beaucoup pour cette étincelle !