Inequality

[Branza]

can somebody solve this problem:
if

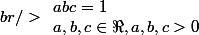
then prove:

plz try to solve it en english becoz i can't understand france
i need it today
thanks

[Clembou]

can somebody solve this problem:
if

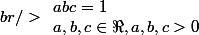
then prove:

plz try to solve it en english becoz i can't understand france
i need it today
thanks

In the last topic, the question was :

Is this problem in connection with trigonometry of the unspecified triangles?

[Weensie]

All right . Are you familiar with usual inequalities such as Chebychev's , nesbitt ,Holder , Cauchy schwartz etc... ?

[Branza]

All right . Are you familiar with usual inequalities such as Chebychev's , nesbitt ,Holder , Cauchy schwartz etc... ?

only what i want is to solve this problem,i try a lot of but i didnnt succeed
maybe you could.plz solve it if you know to solve it.

[Weensie]

I may have not have the time right now . but yet you can consider a , b ,c as complex numbers .
You may know this equation a² + b² + c² = ab + ac + bc defines an equilateral triangle ABC (a,b,c) in the complex plane .
I think you can start from here.

[Weensie]

in general it is :a²+b²+c²>(or=) ab+ac+bc .

[Branza]

I may have not have the time right now . but yet you can consider a , b ,c as complex numbers .
You may know this equation a² + b² + c² = ab + ac + bc defines an equilateral triangle ABC (a,b,c) in the complex plane .
I think you can start from here.

yes i try with this method but nothing,it's too difficult and i must solve it

[Weensie]

So do it . I won't do it until tomorrow morning . So try to focus on the thing unless someone does it for you tonight . I gotta go . see ya

[Zweig]

The inequality to show rewrites like :



From Schur's inequality we have :

Indeed : with

But from AM-GM.

Conclusion follows.

[Zweig]

I may have not have the time right now . but yet you can consider a , b ,c as complex numbers .
You may know this equation a² + b² + c² = ab + ac + bc defines an equilateral triangle ABC (a,b,c) in the complex plane .
I think you can start from here.

a,b,c des nombres complexes ? L'énoncé précise bien que ce sont des réels :marteau:

[Weensie]

Ah oui tu as raison Zweig .
Le passage par l'inégalité de schur dans ce cas était fondamental !
Ceci dit pourrais tu me démontrer a²+b²+c²=ab+ac+bc abc étant les affixes des sommets d'un triangle equilatéral ?

[Branza]

The inequality to show rewrites like :



From Schur's inequality we have :

Indeed : with

But from AM-GM.

Conclusion follows.

you are very good
But one guestion what mean:
AM-GM????

[Zweig]

Humm, je ne connais rien dans les complexes (enfin juste les bases) parcontre je pourrais te montrer que si et seulement si a, b et c sont les côtés d'un triangle équilatéral.



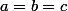
Réciproquement, avec égalité lorsque. "Conclusion follows"

[Zweig]

you are very good
But one guestion what mean:
AM-GM????

It means "Arithmetic means - Geometric means", that's :

For all positive reals and positive intenger , we have :

[Branza]

It means "Arithmetic means - Geometric means", that's :

For all positive reals and positive intenger , we have :

Yes i know that it's inequality between "arithmetic average" and "geometric average"
ab>=2sqrt(ab)
tks very much for help and explanation.i hope that you will understand me.

[Zweig]

Yes I understand you, it's ok :++:

[Matt_01]

Salut !

Que dit l'inégalité de Schur ? Et comment peut on en tirer l'inégalité de la seconde ligne ?

Merci de m'éclairer :id:

[Zweig]

L'inégalité de Schur :

Pour tous réel positifs , et et tout réel on a :



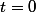
En prenant , on obtient :

[Matt_01]

Euh, désolé, mais comment vient l'équivalence ?

[miikou]

Ah oui tu as raison Zweig .
Le passage par l'inégalité de schur dans ce cas était fondamental !
Ceci dit pourrais tu me démontrer a²+b²+c²=ab+ac+bc abc étant les affixes des sommets d'un triangle équilatéral ?

salut,
d'après l'inégalité du réordonnement a²+b²+c² sup ab+bc+ca



donc a=b=c