Faction trigonométrique

[jentitbeurk]

bonjour je ne comprend vraiment rien a cet énoncé pouvez vous m'aider


a) Mettre sous la forme d'un produit de facteurs chacune des expression
et

b) en déduire une transformation de de la fraction




c) Rendre calculable par logarithme l'expression




Merci d'avance pour votre aide

[MacManus]

Bonjour

a)
En supposant que , x appartient alors à \
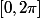
On peut factoriser chacune des expressions par cos(x).

b)
Je retombe avec ces factorisations sur l'expression

[oscar]

Bonjour


E =( cos x +sin x)/( cos x -sin x)

Pour démontrer E' on divise tous les termes de E par cos x#0

[asfah]

cosx+sinx=rac(2)[rac(2)/2*cosx+rac(2)/2*sinx]
=rac(2)[cos(pi/4)*cosx+sin(pi/4)*sinx]
=rac(2)*cos(pi/4 +x)
de la meme maniere on peut montrer que:
cosx-sinx=rac(2)*cos(pi/4 -x)
=rac(2)*sin[pi/2-(pi/4 -x)]
=rac(2)*sin(pi/4+x)
ainsi cosx+sinx/cosx-sinx=cos(pi/4 +x)/sin(pi/4 +x)
=1/tg(pi/4 +x)
rac(2) veut dire la racine de 2

[oscar]

Bonjour


Ta solution est FAUSSE
1ère méthode
E=
[ cos x - cos (pi/2-x)]/[ cos x + ccos (pi/2-x)]

Aplpliquer les formukes cos a -cosb et cos a + cos b où a=x et b =pi/2-x

2e méthode

E' = ( 1-tgx)/(1+tgx)
Appliquer la formule tg (a-b) = (tga -tgb)/(1-tga tg b) et RECIPROQUEMENT
où a = pi/4 et b = x


S.V.P. LAISSEZ-LES CHERCHER