[Nafu_De_Binouze]

Bonjour à tous!! =)

J'aurai besoin d'aide en ce qui concerne les moments d'une variable aléatoire X qui suit une loi de Poisson.

P(X=k) = exp(-E) . (E^k)/(k!)

= Somme (sur k) [ P(X=k) .(k^n)]

Je dois trouver le moment d'ordre 2 qui vaut, selon mon prof: = E² + E.
Seulement je n'arrive pas à aboutir. :mur:

Voici ce que j'ai:

= Somme [ k² . exp(-E) . (E^k)/(k!) ]
= exp(-E) . Somme [ k . (E^k)/(k-1)! ]

Ensuite???


Merci d'avance pour votre aide, et désolée pour la lisibilité de mon post qui n'est vraiment pas terrible!
Bonne journée!



MAJ le 05.06: J'ai trouvé la solution... il faut remplacer k par k= (k-1)+1 et ensuite on tombe sur le DL de exponentielle...et on peut conclure!
A bientot peut etre!

[MacManus]

Bonsoir

Est-ce que tu utilises les "fonctions génératrices" pour calculer les moments ??

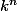
Si c'est le cas, je ne comprends pas bien la présence du k dans de la formule ...
je pense que ce k doit être un paramètre (autre que k lui-même donné en indice, puisque tu fais la somme sur k )...

En gros, moi j'écris par exemple :
où s est un paramètre appartenant à l'intervalle [0,1].

En fait c'est ce que j'utilise en cours, mais je me trompe peut-être...