Fuseau/angle/sphère...

[mathic]

Voilà le titre n'est peut-être pas très explicite mais j'ai pas trouvé mieux ^^

Considérons une sphère que je découpe avec 3cercles distincts en 8triangles sphériques géodésiques (par exemple sur la terre les 3cercles pourraient être l'équateur et 2hémisphères).
Je vais pouvoir considérer alors des fuseaux (au nombre de 4).
Mon prof m'a dit que la surface de chaque fuseau était égale à 2*l'angle qui est le sommet du fuseau... (la surface dépend du rayon du cercle mais ici on considère le rayon égale à 1 pour faciliter).


Je dois donc démontrer cette égalité: en gros (peut-être que mon message est pas très clair) comment démontrer le rapport entre la surface du fuseau et la valeur de l'angle...
Est-ce une formule? peut-on la démontrer?


Merci

[busard_des_roseaux]

Bonsoir,

- L'angle au centre,dans un plan équatorien , vaut l'arc qu'il intercepte (en radians, sur la sphère unité, même chose qu'en trigonométrie plane).
- Les vecteurs tangents, au pôle Nord, forment l'angle C du triangle,
Le vecteur tangent, au pole nord C, sur l'arc (CA) est colinéaire au vecteur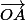 d'origine O le centre de la sphère:
d'où l'angle C du triangle ABC a pour mesure l'arc de grand cercle c=(AB).


on va montrer la formule de l'aire du triangle ABC:


ça se fait en additionnant judicieusement les aires des 8 triangles.
Soient A,B,C formant triangle et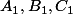 les points antipodaux.

etc..


l'aire de la calotte formée des triangles ABC et CAB1 est proportionnelle
à (l'ouverture de) l'angle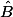 . On en déduit:

en faisant une règle de trois entre les valeurs d'aires et

Par permutation circulaire:



De plus la somme des 8 triangles donne l'aire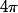 de la sphère,

on regroupe en quatre paires de triangles antipodaux
(ex ABC et de même aire)



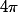étant l'aire de la sphère.

On calcule alors l'aire de la demi-sphère uniquement avec les triangles du pole Sud (BC=cercle équateur).



Comme (triangles antipodaux)
en soustrayant membres à membres les égalités,
il y a beaucoup de simplification et l'on trouve:






Cordialement,

[busard_des_roseaux]

re,


appliquée à un fuseau de pole nord C, la formule d'aire d'un triangle donne:




L'aire du fuseau est donc le double de l'angle du pole nord C.
Pour la sphère unité, les mesure d' "angles", les longueurs et les aires jouent le même rôle . Ensuite, pour une sphère de rayon r quelconque, les angles , qui sont mesurés en radians sur les cercles unités, restent constants par l'homothétie vectorielle , les aires sont multipliées par 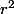et les distances géodésiques, longueurs d'arc, sont multipliées par .

On adapte les formules au cas quelconque.


PS: pour la petite histoire, il me semble que Gauss songeait à mesurer
de très grands triangles pour connaitre la courbure de l'espace (le défaut d'euclidianité des triangles dépend de cette courbure).

[mathic]

Bonsoir, tout d'abord merci d'avoir pris le soin de répondre en ayant de plus prolongé le développement au delà de mes attentes.
J'avais réussie à calculer l'air des triangles avec l'aide de cette formule

l'aire de la calotte formée des triangles ABC et CAB1 est proportionnelle
à (l'ouverture de) l'angle . On en déduit:

Pour cette "formule" je voulais justement savoir comment la démontrer pour la suite du raisonnement.
J'ai pu continuer votre raisonnement à peu de choses près de la même façon en prennant cette formule qu'on m'avait donné, seulement j'aimerais savoir si je peux m'en servir comme d'un acquis (comme une formule qui serait "la somme des angles d'un triangle = 180°" sans justifier cette formule) ou bien si je dois la démontrer par soucis de rigueur (et dans ce cas Comment la démontrer).


merci

[busard_des_roseaux]

J'avais réussi à calculer l'aire des triangles avec l'aide de cette formule
Pour cette "formule" je voulais justement savoir comment la démontrer pour la suite du raisonnement.

1) Il est possible de calculer à la main le volume d'une sphère, par une intégrale de Riemann. C'est fait dans le livre de Terracher de Terminale.

2)Sur la sphère, on peut définir les ensembles mesurables comme la tribu engendrée par les traces de boréliens de .

Les aires,elles, sont déterminées par homothétie, de centre O,centre de la sphère.

Les volumes étant connus, on obtient les aires par:



En dérivant:

A(r)=V'(r)

Cette formule donne par exemple:



Evidemment, c'est insatisfaisant car cela nécessite de considérer la sphère
comme une surface (variété) plongée dans l'espace euclidien de dimension 3 et non pas comme une surface obtenue grâce à un atlas, par recollement de cartes.

Historiquement,nul besoin de l'Espace pour cartographier la Planète. :zen:

[mathic]

Merci mais je voulais juste savoir d'où sort la formule qui dit que la surface d'un fuseau est égale à 2fois l'angle.
Si je pouvais dans un raisonnement le tenir pour acquis ou si je devais justifier cette formule en la démontrant (et donc si démonstration il y a comment le faire).


Merci

[busard_des_roseaux]

Merci mais je voulais juste savoir d'où sort la formule qui dit que la surface d'un fuseau est égale à 2fois l'angle.
Si je pouvais dans un raisonnement le tenir pour acquis ou si je devais justifier cette formule en la démontrant (et donc si démonstration il y a comment le faire).


Merci

le fuseau est la réunion deux triangles ayant un côté commun sur l'équateur.

[mathic]

justement, pourquoi la surface du fuseau est égale à 2fois l'angle du "sommet non commun" ?