bonjour,
cela fait deja pas mal de temps que je cherche a etudier(sans succes) la continuite,et la differentiabilite de:
f(x,y)=(1-cos(x*y))/(x^2+y^2) si (x,y)non=(0,0)
f(x,y)=0 si (x,y)=(0,0)
merci beaucoup d avance
Differentiabilite
2 messages
- Page 1 sur 1
par busard_des_roseaux » 26 Fév 2008, 15:34
bjr,
F est de classe
en dehors de l'origine comme composée de fonctions
Montrons que f est différentiable en l'origine.
=0=f(0,y))
Ceçi prouve que la différentielle de f, en l'origine, si elle existe, ne peut être
que nulle.
Il reste à montrer que f est diiférentiable à l'origine, ie, que
=o(||(h,k)||))
où le "petit o" est la notation de Landau
En passant en coordonnées polaires:
)
)
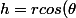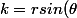=g(r,\theta)=\frac{1}{r^2} \left( 1 - cos( \frac{r^2}{2} \sin(2 \theta)) \right))
Un développement limité selon la quantité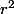
quand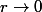 
montre que
=o(r)=o(||(h,k)||))
CQFD.
F est de classe
Montrons que f est différentiable en l'origine.
Ceçi prouve que la différentielle de f, en l'origine, si elle existe, ne peut être
que nulle.
Il reste à montrer que f est diiférentiable à l'origine, ie, que
où le "petit o" est la notation de Landau
En passant en coordonnées polaires:
Un développement limité selon la quantité
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :