Dm

par **noemy** » 16 Oct 2007, 18:53

:help:
je n arrive pas a faire cette exercice de mon devoir pour demain:
DAns le plan muni d un repere,representer l ensemble des points dont les coordonnées (x;y) sont solutios de l equation 4x²-y²<0
donner quatre exemples de couples solutions de cette inequation.
est ce que quelqun peut m aider rapidement??? :help:
j ai oublié de presisé que j ai reussi a s implifier :
(2x-y)(2x+y)<0
que j ai trouvé
y=2X ou y=-2x
et que j ai placé les deux droite dans le repere mais je ne comprend pas comment trouver les solutions

par **ganovar** » 16 Oct 2007, 19:02

Bonjour,

D'abord on commence par le plus simple, d'abord tu résous : 4x²-y²=0

Tu dois avoir deux droites.

Ensuite c'est du régionnement dans le plan. Je te laisse travailler.

Cdlt,

par **noemy** » 16 Oct 2007, 19:13

j ai oublié de presisé que j ai reussi a s implifier :
(2x-y)(2x+y)<0
que j ai trouvé
y=2X ou y=-2x
et que j ai placé les deux droite dans le repere mais je ne comprend pas comment trouver les solutions

par **ganovar** » 16 Oct 2007, 19:16

[quote="noemy"]j ai oublié de presisé que j ai reussi a s implifier :
(2x-y)(2x+y) 0

ou
2x-y > 0 et 2x+y < 0

Tu peux donc hachurer deux régions. Je te laisse poursuivre.

Cdlt,

par **noemy** » 16 Oct 2007, 19:44

je n arrive toujours pas à comprendre
est ce que je dois faire deux graphiques?
car si je met tout cela sur un graphique tout est hachuré

par **ganovar** » 16 Oct 2007, 20:00

[quote="ganovar"]
deux cas possibles:
2x-y 0

ou
2x-y > 0 et 2x+y 2x tu es donc au dessus de

et
y > -2x tu es donc au dessus de

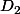
Hachurer la région au dessus de

et au dessus de

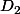
ne devrait pas te poser problème :happy2:

Je te laisse continuer.

Cdlt,

par **noemy** » 16 Oct 2007, 20:19

merci bcp je pense avoir reussi :id:

Dm

Dm

Qui est en ligne