Exo propriété par récurrence- Aide urgente !!!!!

[Katou]

Bonjour, j’ai vraiment besoin d’aide. Je suis bloqué sur quelque chose de surment idiot mais bon…

[b]La suite (Un) est définie par u_1=1/2 et pour tout entier naturel n ≫1 : U_(n+1)= (n+1)/2n u_n .
Démontrer par récurrence que pour tout entier naturel n ≫1 que U_n= n/2^n .

Ce que j’ai fait :
Pour tout entier naturel n ≫1, P(n) est la propriété :
« U_n= n/2^n »
Initialisation : pour n=1 alors u_1=1/2^1 =1/2 . La propriété P(1) est donc vraie.
Hérédité : Suppposons que pour tout entier naturel n ≫1, la propriété P(n) est vraie, c’est-à-dire que U_n= n/2^n .
On démontre alors que P(n+1) est vraie c’est-à-dire que U_(n+1)= (n+1)/2^(n+1) , or U_(n+1)= (n+1)/2n u_n . Ainsi d’après l’hypothèse de récurrence on a :
U_(n+1)= (n+1)/2n× n/2^n

Et là à partir de là je ne sais pas comment résoudre l’hérédité, je serais vraiment reconnaissant si quelqu'un m'éclaire sur le sujet !

[catamat]

Bonjour
Il suffit de simplifier par n puis de regrouper les puissances de 2

[catamat]

Ceci dit il serait bon d'utiliser la balise tex pour une meilleure lisibilité

ici u_n=\dfrac{n}{2^n} si on le met entre balises tex cela donne


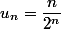
etc...

[Azrabin]

Bonjour,
Attention ta rédaction de l'hérédité est incorrecte, tu ne peux pas écrire" supposons que pour tout...". En effet, si tu supposes que P(n) est vraie pour n'importe quel rang n, P(n+1) est automatiquement vraie donc tu ne démontres rien du tout. Il vaut mieux écrire : "Soit n un entier naturel, on suppose que P(n) est vraie, montrons que P(n+1) est vraie" ou bien "Supposons que P(n) soit vraie pour un rang n donné, montrons que P(n+1) est vraie." Ce sont des exemples de rédaction et plein d'autres sont possibles mais dans tous les cas il est important de ne pas supposer que P(n) est vraie pour tout n puisque c'est précisément ce qu'on cherche à montrer.