(1+x/n)^n
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MaximusvcUcl
- Membre Naturel
- Messages: 22
- Enregistré le: 18 Déc 2021, 19:28
-
par MaximusvcUcl » 18 Avr 2022, 12:40
Bonjour à tous,
Dans le cadre d'un gros projet j'ai besoin d'expliquer une démonstration du mathématicien Edelman.
Voici ce qu'il note :
On définit
=\frac{1}{n\pi}\sqrt{\frac{n^4}{x^2(2n+x)^2}-\frac{(n+1)^2(1+x/n)^2n}{((1+x/n)^{2n+2}-1)^2}})
.
En remarquant que
^n=e^x(1-\frac{x^2}{2n})+O(1/n^2))
, lorsque n tend vers l'infini on a :
=\rho_{\infty}(x)+(\frac{x(2-x)}{2n}\rho_{\infty}(x))'+O(1/n^2))
où
=\frac{1}{2\pi}\sqrt{\frac{1}{x^2}-\frac{4e^{-2x}}{(1-e^{-2x})^2}})
Mes problèmes sont les suivants,
1. D'où sort cette égalité pour
^n)
?
2. Peut on expliciter les termes formant O(1/n^2) ? Le but étant enuite d'intégrer cette fonction mais rien ne prouve que O(1/n^2) est intégrable... J'aimerais donc remplacer ceci par une fonction f(x) dépendante de x pour pouvoir ensuite l'intégrer et arriver au terme O(1/n^2).
3. Qlq saurait-il me guider afin de montrer que l'égalité entre nos deux fonctions rho est bien juste ?
Merci d'avance !
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
par lyceen95 » 18 Avr 2022, 12:54
Je pense que tu peux t'appuyer sur le triangle de Pascal.
Le triangle de Pascal te donne facilement les 3 ou 4 premiers termes du développement de
^n)
Les termes suivants sont inutiles, car négligeables.
Et à côté, il te faut aussi un développement limité de
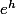
si tu as besoin de garder le 1er terme comme il est dans ta formule.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
