Rendement optimal

[Nikogil]

Bonjour.
J'ai un problème que j'arrive pas à mettre en équation de façon à pouvoir le résoudre.
Pouvez vous m'aider?

J'ai une valeur v qui produit des intérêts i a un taux annuel t.
Pour quelle valeur de i je peux ajouter i à v pour obtenir un gain optimal sachant que lors de cette capitalisation des intérêts, des frais f sont à soustraire à i.
Pour résumer j'ai un capital de départ qui produit des intérêts a un taux fixe que je peux capitaliser quand je veux, moyennant des frais fixes. Je veux trouver les moments opportuns quand capitaliser ces intérêts de façon à faire croître le capital le plus rapidement possible.
Je sais déjà que i>f de façon évidente mais ça s'arrête là.

Merci pour votre aide.

[Ben314]

Salut,
La façon dont je vois le bidule :
Si représente les intérêts obtenus à chaque période et qu'on choisi de capitaliser au bout de périodes, on se retrouve avec une nouvelle valeur égale à 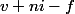, c'est à dire une multiplication de par 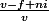pour les périodes ce qui équivaut à une multiplication par à chaque période.
Et c'est ce qui doit être maximum.
Si on dérive en , on obtient une équation dont on ne sait pas exprimer la solution exacte à l'aide des fonction élémentaires, mais on peut évidement l'approximation. On peut aussi directement chercher le max. de en calculant sa valeur pour 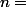1,2,3,...