La n-ième dérivée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MaximusvcUcl
- Membre Naturel
- Messages: 22
- Enregistré le: 18 Déc 2021, 19:28
-
 par MaximusvcUcl » 15 Jan 2022, 10:55
par MaximusvcUcl » 15 Jan 2022, 10:55
Bonjour à tous/toutes,
Je cherche la norme uniforme sur [0,1] de la n-ième dérivée de la fonction
=\frac{1}{1+2x})
.
Pour ce faire je pensais utiliser le fait que cette fct est équivalente à la série géométrique :
^n)
Que faire ensuite ?
Merci !
Modifié en dernier par
MaximusvcUcl le 15 Jan 2022, 11:23, modifié 1 fois.
-
mathelot
 par mathelot » 15 Jan 2022, 11:10
par mathelot » 15 Jan 2022, 11:10
Bonjour,
calcule les dérivées
})
puis essaye de démontrer la formule à trouver par récurrence sur l'entier n.
Abandonne la série qui ne donne que des nombres dérivés de f en x=0
-
MaximusvcUcl
- Membre Naturel
- Messages: 22
- Enregistré le: 18 Déc 2021, 19:28
-
 par MaximusvcUcl » 15 Jan 2022, 11:22
par MaximusvcUcl » 15 Jan 2022, 11:22
Merci pour ta réponse, mais j'ai oublié de préciser que justement la dérivée en x=0 nous intéresse car on cherche la norme uniforme pour
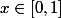
-
mathelot
 par mathelot » 15 Jan 2022, 11:43
par mathelot » 15 Jan 2022, 11:43
on peut identifier (égaliser) les deux séries:
^k)
et
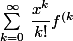}(0))
ce qui donne la formule de
}(0))
sinon démontrer par récurrence sur l'entier n que
}(x)=\dfrac{(-1)^n \, n! 2^n}{(1+2x)^{n+1}})
-
mathelot
 par mathelot » 15 Jan 2022, 12:11
par mathelot » 15 Jan 2022, 12:11
MaximusvcUcl a écrit:Merci pour ta réponse, mais j'ai oublié de préciser que justement la dérivée en x=0 nous intéresse car on cherche la norme uniforme pour
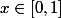
Quelle norme uniforme ?
-
MaximusvcUcl
- Membre Naturel
- Messages: 22
- Enregistré le: 18 Déc 2021, 19:28
-
 par MaximusvcUcl » 15 Jan 2022, 12:18
par MaximusvcUcl » 15 Jan 2022, 12:18
Merci Mathelot pour ta réponse,
Comment tu trouves cette identification ?
Pour la norme uniforme je parle de
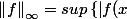 \right | : x\in [0,1]\right \})
-
mathelot
 par mathelot » 15 Jan 2022, 12:57
par mathelot » 15 Jan 2022, 12:57
MaximusvcUcl a écrit:Merci
Comment tu trouves cette identification ?
f est développable en série entière au voisinage de 0 d'une seule manière.
la formule en (-2x)^n vient du développement de la série géométriquede raison (-2x).
la 2eme formule en
}(0))
est sa série de Taylor à l'origine (je crois que c'est la série de Taylor-MacLaurin de f)
quel est le but final de ta question ? que cherches-tu à démontrer ?
-
mathelot
 par mathelot » 15 Jan 2022, 13:31
par mathelot » 15 Jan 2022, 13:31
on a donc:
}(x)| = n! 2^n)
-
MaximusvcUcl
- Membre Naturel
- Messages: 22
- Enregistré le: 18 Déc 2021, 19:28
-
 par MaximusvcUcl » 15 Jan 2022, 19:16
par MaximusvcUcl » 15 Jan 2022, 19:16
C'est ce que je voulais, merci beaucoup !
-
MaximusvcUcl
- Membre Naturel
- Messages: 22
- Enregistré le: 18 Déc 2021, 19:28
-
 par MaximusvcUcl » 15 Jan 2022, 19:36
par MaximusvcUcl » 15 Jan 2022, 19:36
Mathelot, peut-être que tu pourras m'aider pour un autre souci du même genre :
^{(n+1)} \right | : x\in [-2,2] \right \})
Pour
=cos(x)-sin(x))
-
mathelot
 par mathelot » 16 Jan 2022, 00:55
par mathelot » 16 Jan 2022, 00:55
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités