.........

par **sebkillerman** » 18 Déc 2006, 16:44

.................................

par **maturin** » 18 Déc 2006, 16:49

alors faudrait nous dire ce que c'est que P.

Sinon la tangeante en x0 à une courbe d'équation y=f(x) a pour équation
y=f'(x0)(x-x0)+f(x0)

par **sebkillerman** » 18 Déc 2006, 16:57

Oupps désole donc P est une parabole d'équation y=x²/4.

par **maturin** » 18 Déc 2006, 17:35

a)
alors ta tangeante à P en A passe par A
donc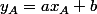

avec

et

et la pente de la tangeante est égale à la dérivée de P(x) en

Donc a=P'(x_0)
P'(x)=(2x)/4=x/2

donc

tu as donc bien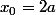

et

=>

b) ce qu'on a fait montre que la tangeante au point x0 a pour équation y=ax-a² avec a=x0/2
ça montre aussi la reciproque et la conclusion.

4) a) racine commune t=2 si tu le trouves pas de façons évidente tu applique la méthode du discriminant pour trouver toutes les racines.

b) je ne sais pas ce que tu appelles un point associé à une équation...

par **greg03** » 18 Déc 2006, 20:55

j'ai le meme dm pour demain!
concernant le 4)b) il n'y a pas d'autre explications moi aussi je trouve ca bizarre...
si ca peut t'aider voici le début de l'énoncé:
1) pour tout point M(x;y) on associe t²-xt+y=0 (E)
a)demontrer que x²-4y>0 equivaut a (E) a 2 racines distinctes
b)tracer la parabole P y=x²/4
2) T point de P d'abscisse m prouver que la tangente a P en T a pour equation y=(m/2)x-m²/4
je n'ai pas bien compris ton explication du 4)a)

par **greg03** » 18 Déc 2006, 21:51

Il y a quelqu'un?

.........

.........

Qui est en ligne