Bonjour, j’ai presque terminer mon DM sur le nombre d’or mais je sèche sur les deux dernières questions:
On a
•U(n) correspondant à la suite de fibonacci donc avec U(1)=U(2)=1 et U(n+2)=U(n+1)+U(n)
•V(n)=U(n+1)/U(n)
•V(n+1)=1+1/V(n)
Q°1 Montrer que V(n) est strictement positive
Q°2 On suppose que la suite V(n) converge.Calculer sa limite
Ps: pour la question 2 je sais que la limite est le nombre d’or mais je ne sais pas comment le démontrer.
Pourriez vous m’aidez svp !!
Suite Fibonacci
4 messages
- Page 1 sur 1
Re: Suite Fibonacci
Bonjour,
Pour montrer que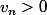 on utilise le fait que c'est une fraction de termes strictement positifs (la suite de Fibonacci est croissante et son premier terme est 1)
on utilise le fait que c'est une fraction de termes strictement positifs (la suite de Fibonacci est croissante et son premier terme est 1)
Pour calculer la limite, vous devez utiliser le théorème du point fixe : si la fonction f est continue, et si la suite) est définie par la relation de récurrence
est définie par la relation de récurrence 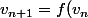) et si la suite converge, alors sa limite est un point fixe de f, c'est-à-dire vérifie
et si la suite converge, alors sa limite est un point fixe de f, c'est-à-dire vérifie =a) , théorème que vous avez dû voir en cours.
, théorème que vous avez dû voir en cours.
Pour montrer que
Pour calculer la limite, vous devez utiliser le théorème du point fixe : si la fonction f est continue, et si la suite
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Suite Fibonacci
hdci a écrit:Bonjour,
Pour montrer queon utilise le fait que c'est une fraction de termes strictement positifs (la suite de Fibonacci est croissante et son premier terme est 1)
Pour calculer la limite, vous devez utiliser le théorème du point fixe : si la fonction f est continue, et si la suiteest définie par la relation de récurrence
et si la suite converge, alors sa limite est un point fixe de f, c'est-à-dire vérifie
, théorème que vous avez dû voir en cours.
MERCI BEAUCOUP!
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
