Bonjour,
Je dois approximer par calcul de différentielles différentes valeur et je n'arrive pas à le faire pour 0,99^4. de meme pour 0,95^4.Pouvez vous m'aider svp
Différentielles
11 messages
- Page 1 sur 1
Re: Différentielles
f(1-h)=f(1)-hf'(1)+o(h)
Précise ce que tu as appris et qui ressemble à ce que je t'ai proposé.
Précise ce que tu as appris et qui ressemble à ce que je t'ai proposé.
Re: Différentielles
Tout d'abord merci beaucoup pour votre aide  néanmoins en cours on m'a apppris de me rapprocher d'une forme dérivé connue. Or ici avec les exposant 4 je ne sais pas trop comment faire.
néanmoins en cours on m'a apppris de me rapprocher d'une forme dérivé connue. Or ici avec les exposant 4 je ne sais pas trop comment faire.
Re: Différentielles
Si biensur mais je ne vois pas vraiment le rapport avec ce que tu trouves. Comment sais-tu qu'il faut faire ca directement. Merci pour ton aide
Re: Différentielles
Différentielle pour approximer, dis-tu.
f(a+h) = f(a) + ???
Et tu ne vois pas le rapport avec
(1-0.01)^4 = ???
Vraiment ?
f(a+h) = f(a) + ???
Et tu ne vois pas le rapport avec
(1-0.01)^4 = ???
Vraiment ?
Re: Différentielles
oui je ne comprend pas vraiment nous sommes censés simplifier afin de pouvoir calculer de tete
Re: Différentielles
Bon, je remplis les points d'interrogation puisque tu n'as pas l'air parti pour le faire.
Tu connais peut-être la formule de Taylor avec reste de Lagrange. Elle dit que pour tout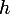 il existe
il existe  tel que:
tel que:
 = f(a) + h f'(a) + \dfrac{h^2}{2} f''(a+\theta h))
En gros, ça dit que l'erreur que l'on fait en remplaçant) par
par  + h f'(a)) (où
(où 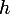 est petit) est de l'ordre de
est petit) est de l'ordre de  (donc très petit).
(donc très petit).
Application :
^4 \simeq {??})
Ici qui est a ? qui est h ? qui est f ?
Tu connais peut-être la formule de Taylor avec reste de Lagrange. Elle dit que pour tout
En gros, ça dit que l'erreur que l'on fait en remplaçant
Application :
Ici qui est a ? qui est h ? qui est f ?
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
