Biostatistiques 2

[Batteur]

Bonjour je me permet d'écrire une nouvelle question concernant un exercice de statistique qui me bloque un peu.
* On veut calculer l'intervalle de confiance pour la moyenne de la température maximale, des enfants avec grippe, si on a les données sur un échantillon de 11 sujets. La valeur de la quantile d’ intérêt est 2,23. La moyenne de la température est égale à 39 et l'écart type d’ échantillonnage =0,8 Quelle est l'intervalle de confiance à 95 % pour la température moyenne de la population ?
A) [38,41;38,59]
B) [38,46;39,54]
C) [38,5;39,5]
D) [38,53;39,47]
E) [38,44;39,56]
réponse vraie: B. Moi je trouve la réponse E) donc j'aimerais savoir où je me suis trompé.
n=11
DS=0.8
m=39
Mon cours dit que pour estimer un paramètre de la population avec n<30 on utilise
m+/- t(n-1,alpha/2) *(s/racine(n-1))
donc 39-t(10,0.05/2)*(s/racine(10) pour t=2,228 ici ils donnent 2,23
Comment fait on pour calculer s ? est ce qu'on utilise bien 0.8?
Si j'ai fais une erreur dans mon calcul veuillez me l'indiquer svp merci.

[LB2]

Bonjour,

On détermine une fourchette de valeurs plausible de la vraie moyenne dans la population en déterminant toutes les valeurs qui ne sont pas rejetées par le test t de Student pour n=11. Ici la quantité d'intérêt (et non la quantile) vaut t=2.23 à 0.01 près. Cela correspond à la valeur critique du test t de Student pour n=11, donc 10 d.d.l. et alpha = 5%.

Les valeurs ne sont pas rejetées si elles vérifient l'inégalité

avec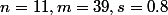

soit l'intervalle de confiance [38.46, 39.54]

[Batteur]

Ah d'accord je comprends mieux, mais du coup il faut que j'essaye au moins une valeur de chaque intervalle proposé pour voir si cela correspond à la valeur 2.23 ? J'ai essayé le calcul et effectivement quand j'applique la formule avec la valeur 39,54 par exemple je tombe sur 2,23. Merci

[LB2]

Non, on te donne la valeur 2.23, il faut que tu calcule les valeurs limites de x, qui correspondent au cas d'égalité de l'inégalité.

[Batteur]

D'accord mais comment calcul t-on les valeurs limites de x ? avec quelle formule ?

[LB2]

C'est la formule de ton cours, que j'ai également rappellée :

l'intervalle de confiance est de la forme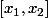

avec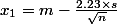
et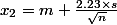

La valeur 2.23 correspond à t(n-1,alpha/2) pour n=11 et alpha = 5%.

Attention, vérifie la formule de ton cours, pour moi c'est bien diviser par un facteur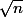 et pas qui donnerait un intervalle de confiance légèrement différent.

[Batteur]

Merci pour votre aide, je n'avais effectivement pas ces formules dans mon cours et concernant la formule que j'ai énoncée au début, c'est bien ce qui est écrit dans mon cours concernant l'estimation d'un paramètre sur la population pour une moyenne avec n<30 mais effectivement il y a également écrit la formule m+/- Z(alpha/2)*(s/racine (n)). Vu que ce n'est pas précisé quelle formule est la plus adaptée, j'ai donc utilisé celle-ci. Merci

[LB2]

Effectivement, la légère différence s'explique car ici on n'est pas dans un problème d'estimation de paramètre, mais bien d'établissement d'intervalle de confiance