Limite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MathEtO
- Messages: 8
- Enregistré le: 01 Déc 2019, 12:43
-
 par MathEtO » 01 Déc 2019, 12:55
par MathEtO » 01 Déc 2019, 12:55
Bonjour, je cherche la limite de

en

.
J'ai essayé de factoriser par
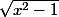
, par

, par

, de passer à l'exponentielle du logarithme, de multiplier par l'expression conjuguée mais je n'arrive pas à lever l'indétermination.
Merci d'avance pour votre aide.
-
mathelot
 par mathelot » 01 Déc 2019, 13:38
par mathelot » 01 Déc 2019, 13:38
 =\dfrac {x^2-2x+1-(x^2-1)}{x-1+\sqrt{x^2-1}}<br />=\dfrac{-2x+2}{x(1-\dfrac{ 1}{x}+\sqrt {1-\dfrac{1}{x^2}})})
La limite est donc-1
La technique est claire:factoriser les termes dominants
-
MathEtO
- Messages: 8
- Enregistré le: 01 Déc 2019, 12:43
-
 par MathEtO » 01 Déc 2019, 14:59
par MathEtO » 01 Déc 2019, 14:59
Effectivement il ne me manquait pas grand chose...
Merci beaucoup pour votre aide !
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 01 Déc 2019, 20:05
par pascal16 » 01 Déc 2019, 20:05
on peut aussi mettre x en facteur de la racine
faire un DL1 de la racine de 1-1/x en 1 car 1/x tend vers 0
et retrouver le même résultat
-
mathelot
 par mathelot » 01 Déc 2019, 21:29
par mathelot » 01 Déc 2019, 21:29
effectivement, la méthode que j'ai exposée est de niveau terminale S, sinon , dans l'enseignement post-bac,
on fera plutôt des développements limités (DL) comme le conseille @pascal16
-
MathEtO
- Messages: 8
- Enregistré le: 01 Déc 2019, 12:43
-
 par MathEtO » 02 Déc 2019, 12:46
par MathEtO » 02 Déc 2019, 12:46
Merci pour l'info, j'essaierai d'y penser quand j'aurais vu les développements limités.
Merci encore.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6148
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 02 Déc 2019, 13:08
par GaBuZoMeu » 02 Déc 2019, 13:08
Variante :
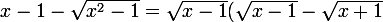=\dfrac{-2\sqrt{x-1}}{\sqrt{x-1}+\sqrt{x+1}}=\dfrac{-2}{1+\sqrt{\dfrac{x+1}{x-1}}})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités