N divisible ?

[Jewgah]

Bonjour,



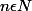
n n'est pas divisible par 2 ni 3 (sous-entendu n'est pas divisible sans reste).

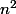
Comment démontrer que est divisible par 24 avec un reste de 23?

Merci d'avance pour votre aide

Jewgah

[lyceen95]

Essaie quelques nombres, pour voir un peu comment ça marche.
Par exemple pour n = 5 ou n=7.
Et tu devrais voir que l'énoncé est faux, et tu devrais même trouver quelle est la correction qu'il faut apporter à l'énoncé .... pour le transformer en un énoncé correct.

[Jewgah]

Salut!
Merci pour ton message mais je me permets de penser que tu n'as pas compris l'énoncé.

En remplaçant n j'obtiens:

[pascal16]

est divisible par 24 .... divisible par 24; à la base dit que n est un multiple de 24
... avec un reste de 23? on remplace divisible par divisé et ça donne un truc plus juste

ce que tu écris, c'est que n²+23 est divisible par 24

n²=49 =2*24+1 quand on fait une division euclidienne par 24, le reste est 1.

[GaBuZoMeu]

@jewgah : l'énoncé que tu donnes n'est pas très bien formulé, mais on comprend que si n'est divisible ni par 2 ni par 3, alors son reste dans la division euclidienne par 24 est 23. Ceci est faux, bien sûr, le reste est 1.

Ça peut se voir avec les restes chinois : le seul carré inversible modulo 8 est 1, le seul carré inversible modulo 3 est 1, donc le seul carré inversible modulo 24 est 1. Ça dit exactement que pour tout entier premier avec 24 (c.-à-d. divisible ni pas 2 ni par 3), est congru à 1 modulo 24.