Norme d'un vecteur et coordonnées

[MrLan]

Bonjour, j'ai une question d'un travail qui me tiraille un peu. Je sais que c'est très simple, j'ai la formule, mais je n'arrive pas à l'appliquer.

J'ai 3 points
A=(1,2,-3), B=(0,1,4) et C=(-1,0,3)
Premièrement, il faut trouver la distance entre A et B. Bon, c'est plutôt simple, il faut trouver la norme du vecteur AB, donc :

d= SQRT((0-1)exp2 + (1-2)exp2 + (4+3)exp2)
d=sqrt(51)

Pour ça, ça va... du moins, je crois...

Deuxièmement, on demande de trouver un vecteur de norme 3 ayant la même orientation que le "vecteur AB".

Je suis mystifié...

J'ai bien comme formule :

c "vecteur y" / |"vecteur y"| tant que c > 0

c = 3 (c'est OK)

Mais c'est ici que ça se corse

C'est facile à calculer une fois que j'ai mon "vecteur y", mais j'ignore comment déterminer mon "vecteur y" à partir des coordonnées qu'on me donne...

Pouvez-vous m'aiguiller SVP? Ça serait sympa!

Merci, bonne journée!

Mr. Lan

[hdci]

Bonjour,

Si j'ai bien compris, on te demande de trouver un vecteur tel que et avec ?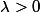

Que vaut alors ? Donc quelle valeur pour ?

[MrLan]

La question exacte est :

Soient les points suivants :
A=(1,2,-3)
B=(0,1,4)
C=(-1,0,3)

Trouvez un vecteur de norme 3 ayant la même orientation que le vecteur ?

Mr. Lan

[pascal16]

Deuxièmement, on demande de trouver un vecteur de norme 3 ayant la même orientation que le "vecteur AB".


de même direction : 3 * "vecteur AB" / norme de AB et -3 * "vecteur AB" / norme de AB
de même direction et sens : 3 * "vecteur AB" / norme de AB

[MrLan]

C'est exactement ce que je pensais vu la formule, mon problème, c'est de calculer "Vecteur AB" à partir des coordonnées que j'ai...

C'est là où je bloque...

Mr. Lan

[pascal16]

A=(1,2,-3), B=(0,1,4)

en vecteur : AB(xB-xA ; yB-yA ; zB-zA) soit "extrémité moins origine".

[MrLan]

Merci, c'est apprécié, j'essaie ça ce midi!

Mr. Lan