Combien de triangles isocèles?

[Prunille]

Bonjour à vous,

Cet exercice me donne du soucis, un coup de main serait le ben venu

voilà l'énoncé:

Combien peut-on construire de triangles isocèles de périmètre 15cm et dont les côtés sont un nombre entiers de cm?

Un grand merci à tout ceux qui m'aideront !

[pascal16]

les cotés font tous de 0 à 15 cm
on a c1+c2+c3=15
si deux sont égaux, on peut gérer à la main les solutions possibles

[Prunille]

Merci pour ta réponse

Oui j'entends bien, mais ce que je comprends pas, c'est comment on trouve combien on en construit...

[mathelot]

on cherche les solutions de


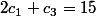
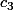
est un nombre impair compris, au sens large, entre 1 et 15

[Prunille]

Merci pour ta réponse^^

J'ai compris cet aspect de la question, c'est la définition même d'un triangle isocèle...

Mais on nous demande combien de triangles isocèles on peut construire, pas la valeur de c3

:3

[pascal16]

on te demande le nombre de valeurs de c3 possible en fait

or c3=15-2c1

c3 est donc un nombre impair entre 0 et 15 si on accepte le triangle plat

il y a combien de valeurs de c3 possibles ?

[Prunille]

Bien..justement, je ne sais pas la réponse...

C'est pour ça que je viens demander de l'aide ici :3

[mathelot]

cites moi des chiffres impairs

[Prunille]

Aaaaaah ok !
^^ je suis bête XD je viens de comprendre...

Merci beaucoup

[Black Jack]

Salut,

Il faut aussi tenir compte que la somme de 2 cotés est > que le 3eme coté

2.C1 + C3 = 15
2 C1 > C3
Avec C1 et C3 dans N*

Et donc, il y a moins de triangles que ceux suggérés.

Pour moi, il y en 4.

[pascal16]

c1€{1;3;5} ?

[Black Jack]

Avec C1 = C2
C3 le 3eme coté :

C3 : 1 , 3, 5 , 7
et C1 = C2 correspondants : 7 , 6, 5 , 4

Non ?

[pascal16]

oui, c'est bon