√(a+b)= ?

[Thrawni]

Bonjour,

Cela fait quelques heures que je bloque sur une racine carré (√(a+b)) puis j'en suis à me poser la question suivante: comment fait on la racine carré d'une parenthèse quand il y une ou plusieurs inconnus ?

Merci d'avance pour vos réponses.

[Lostounet]

Salut,
En général on ne peut rien faire.

La racine d'une somme... c'est la racine de cette somme... sauf cas particulier où on arrive à factoriser la somme en question.

La racine carrée n'aime pas les sommes.

[Thrawni]

Bonsoir,

Tout d'abord, merci pour votre réponse. Moi qui voulais creuser un peu plus la question me voilà très vite arrêter ^^. Je vais alors m'intéresser d'autres choses.

[nodgim]

Parfois, cette écriture peut être utile :
V(a(1+b/a)) = Va * V(1+b/a)

[pascal16]

il y a des cas où on peut faire quelque chose :
√(4a+4b)
=√4 √(a+b)
= 2√(a+b)

avec a>0 : √(a+b)) = √a*√(1+b/a)

[Ben314]

Salut,
Sinon, tant qu'à faire de donner des exemples, l'un des cas "classique" qu'on rencontre où on peut se poser la question de savoir s'il y a moyen d'écrire un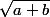 plus simplement, c'est celui de truc du style qui s'avère être égal à ou bien de qui s'avère être égal à alors que , on peut l'écrire autrement, mais pas vraiment "plus simplement".