Salut, c'est les relations "coefficients racines",
si on a un polynôme de degré n
=a_nX^n+...+a_0)
et si on note
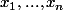
ses racines,
on sait que le polynôme est scindé et qu'il est de la forme
=a_n(X-x_1)...(X-x_n))
On en déduit :
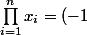^n\frac{a_0}{a_n})
Pour retrouver rapidement ce résultat on regarde ce que l'on obtient lorsque l'on développe P(x) sous forme scindé sans prendre de X, on obtient :
=(*)+a_n(-x_1)(-x_2)...(-x_n))
(où (*) sont les autres termes du polynôme qu'on ne considère pas).
Or comme on sait que les coefficients d'un polynôme sont uniques, on a :
(-x_2)...(-x_n)=a_0)
ce qui donne ce que j’ai écris plus haut.
(dans ton cas ton polynôme est unitaire donc tu n'as pas de

).
[pardon lostounet j'avais déjà écrit mon message quand tu as répondu]
 !!
!!