bonjour, pouvez-vous m'aider à comprendre la correction de cet exercice?
Pour n ∈ N*
, on désigne par N le nombre de diviseurs positifs de n et par P leur
produit. Quelle relation existe-t-il entre n, N et P ?
solution:En associant dans P^2 = P × P chaque diviseur d avec celui qui lui est conjugué
n/d, on obtient un produit de N termes égaux à n. Ainsi
P^2 = n^N .
Arithmetique-divisibilité
5 messages
- Page 1 sur 1
Re: arithmetique-divisibilité
Pour 30 par exemple :
1 2 3 5 6 10 15 30 soit 8 diviseurs, soit 2 fois 4.
On groupe chaque diviseur avec son conjugué :
1 avec 30, 2 avec 15, 3 avec 10, 5 avec 6. Ils ont tous le même produit 30.
Le produit des diviseurs est donc 30*30*30*30 soit n^4, soit n ^ (la moitié du nombre de diviseurs).
P = n ^(N/2) ou P² = n^N.
1 2 3 5 6 10 15 30 soit 8 diviseurs, soit 2 fois 4.
On groupe chaque diviseur avec son conjugué :
1 avec 30, 2 avec 15, 3 avec 10, 5 avec 6. Ils ont tous le même produit 30.
Le produit des diviseurs est donc 30*30*30*30 soit n^4, soit n ^ (la moitié du nombre de diviseurs).
P = n ^(N/2) ou P² = n^N.
Re: arithmetique-divisibilité
salut
Pour comprendre, tu peux voir avec un exemple
soit =30
=30
Les diviseurs de 30: 1, 2, 3, 5, 6, 10, 15, 30 on a N=8
Le produit des diviseurs peut s'écrire:
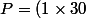\times (2\times 15)\times (3\times 10)\times (5\times 6)=n^4)
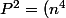^2=n^8=n^N)
A toi de mettre ça en forme dans le cas général !
Pour comprendre, tu peux voir avec un exemple
soit
Les diviseurs de 30: 1, 2, 3, 5, 6, 10, 15, 30 on a N=8
Le produit des diviseurs peut s'écrire:
A toi de mettre ça en forme dans le cas général !
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
