Montrer qu'une fonction est croissante

[yann06]

et

1 - Montrer que f est croissante sur [0;1]

2 - étudier le signe de f(x) - g(x) sur [0;1] et interpréter graphiquement le résultat

3 - Tracer dans un meme repère orthonormé les représentations graphiques des fonctions f et g

-----------------------
1 )
La fonction est croissante sur l'intervalle [0;1] si pour tout nombre a et pour tout nombre b pris dans cet intervalle et rangés tel que a < b

( fonction croissante )

soit et

je cherche donc le signe de la différence et je regarde si














en fait je voudrais démontrer que

Pour cela :

par hypothèse : on a et

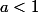
donc en additionnant,
puis

[pascal16]

(a-b)² ne vaut pas (a-b)(a+b) mais (a-b)(a-b)

f(x)=0.96x²+0.04x = x(0.96x+0.04)

f(x)= 0 <=> x= 0 ou x= -0.04/0.96

f est une fonction du second degré, du type a x²+bx+c avec a positif.
elle est donc décroissante puis croissante
f(x)=0 admet -0.04/0.96 et 0 comme solution
elle est donc en forme de U et par calcul de son axe e symétrie, atteint son minimum pour x= (-0.04/0.96 +0 )/2
c'est un nombre négatif, elle est croissante de ce nombre à +oo
elle est donc croissante sur [0;1]


variante :
f(x)=0.96x²+0.04x
0<=a<b
=> 0<=a²<b² et 0<=0.04a < 0.04b
=> 0<= 0.96a²<0.96b² et 0<=0.04a < 0.04b
=> 0<= 0.96a²+0.04 a <= 0.96b² + 0.04 b
=> 0 <= f(a)<f(b)
f conserve l'ordre, elle est strictement croissante sur [0;+oo[ donc sur [0;1] aussi

[Tiruxa47]

Bonjour,

En fait cela donne :



et tu peux continuer comme tu l'as fait puisque a²-b²=(a-b)(a+b)

en fait je voudrais démontrer que

C'est juste du au fait que a et b sont positifs

[yann06]

Bonsoir TIRUXA


oui, j'ai fait une belle erreur dans la factorisation ( j'ai sans doute voulu aller trop vite !)
alors j'ai écrit, effectivement
et là, je doit mettre 0,96 en facteur

ça n'est pas

mais bien sur
puis finalement

[yann06]

j'ai bien compris que puisque a + b sont positifs ( tout cela est très logique, je suis d'accord)

mais là je veux faire la démonstration qui consiste à partir de l'hypothèse : et

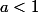
et en additionnant
et là, et bien je n'arrive plus à poursuivre
Pouvez vous m'aidez ? en me faisant réfléchir ( sans me donner la réponse

[yann06]

enfin, en additionnant et

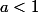
première étape : a + b est forcément inférieur à 2 si on les additionne

[Tiruxa47]

Oui bien sûr mais la majoration n'est d'aucune utilité ici...
Si tu veux, à tout prix, conserver l'encadrement, tu peux partir de :


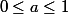
par addition

en multiplant pas 0.96

enfin en ajoutant 0.04