(kx + 1)^2 - 8x = 0
20 messages
- Page 1 sur 1
(kx + 1)^2 - 8x = 0
Bonjour,
est ce que quelqu'un pourrait m'aider à trouver la valeur k pour que l'équation suivante aie une seule solution: (kx + 1)^2 - 8x = 0
en développant (kx + 1) ^2 et en mettant le résultat dans l'équation j'ai obtenu :
kx^2 + 2kx +1 -8x = 0
mais je sais pas comment continuer...
La réponse est k=2
merci!
est ce que quelqu'un pourrait m'aider à trouver la valeur k pour que l'équation suivante aie une seule solution: (kx + 1)^2 - 8x = 0
en développant (kx + 1) ^2 et en mettant le résultat dans l'équation j'ai obtenu :
kx^2 + 2kx +1 -8x = 0
mais je sais pas comment continuer...
La réponse est k=2
merci!
Re: (kx + 1)^2 - 8x = 0
lalia a écrit:k^2x^2 + 2kx +1 -8x = 0
Salut,
Effectivement, k est bien = à 2
Modifié en dernier par laetidom le 21 Oct 2017, 11:24, modifié 1 fois.
Re: (kx + 1)^2 - 8x = 0
lalia a écrit:mais comment je dois faire pour obtenir cette réponse?
lalia a écrit:k^2x^2 + 2kx +1 -8x = 0
Mets sous la forme ax²+bx+c=0
et pour avoir 1 solution on doit avoir
Modifié en dernier par laetidom le 21 Oct 2017, 14:32, modifié 1 fois.
Re: (kx + 1)^2 - 8x = 0
lalia a écrit:k^2x^2 + 2kx +1 -8x = 0
soit
k^2x^2 + (2k - 8)x + 1 = 0
Donc
Comprends-tu ?
Modifié en dernier par laetidom le 21 Oct 2017, 12:03, modifié 1 fois.
Re: (kx + 1)^2 - 8x = 0
en mettant sous la forme ax^2 + bx + c
j'obtiens a = k ; c= 1 mais je ne trouve pas b , ce serait 2k - 8 ?
j'obtiens a = k ; c= 1 mais je ne trouve pas b , ce serait 2k - 8 ?
Re: (kx + 1)^2 - 8x = 0
Pour moi,
Convaincu ?
lalia a écrit:en mettant sous la forme ax^2 + bx + c
j'obtiens a =; c= 1 mais je ne trouve pas b , ce serait 2k - 8 ===> Oui ?
Convaincu ?
Re: (kx + 1)^2 - 8x = 0
lalia a écrit:Merci beaucoup! j'ai enfin réussi!
SUPERBE !! @+ sur le forum !!
Re: (kx + 1)^2 - 8x = 0
Complément :
Vérification avec k=2 on obtient 4x² - 4x + 1= 0 qui donne visuellement :

Vérification avec k=2 on obtient 4x² - 4x + 1= 0 qui donne visuellement :

Re: (kx + 1)^2 - 8x = 0
n'a pas eu sa réponse la-bas : https://www.ilemaths.net/sujet-kx-1-2-8x-757255.html
donc vient voir ici
et lui donner la réponse ne l'aura pas fait travailler ...
donc vient voir ici
et lui donner la réponse ne l'aura pas fait travailler ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: (kx + 1)^2 - 8x = 0
Salut zygomatique,
zygomatique a écrit:n'a pas eu sa réponse la-bas : https://www.ilemaths.net/sujet-kx-1-2-8x-757255.html =====> je n'étais pas au courant,
donc vient voir ici =====> ça n'est pas "répréhensible" je pense, au contraire . . ., lalia cherche à savoir . . . mieux que de faire de la console ou autre . . .
et lui donner la réponse ne l'aura pas fait travailler ... =====> après quelques échanges :=====> ce qui me faisait penser que lalia avait travaillé puis compris . . . c'est mon ressenti, peut-être que je me trompe . . .lalia a écrit:Merci beaucoup! j'ai enfin réussi!
Re: (kx + 1)^2 - 8x = 0
100% d'accord avec Laetidom: c'est pas un crime d'utiliser plusieurs forums..
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: (kx + 1)^2 - 8x = 0
oui, j'avais en effet travaillé plusieurs heures sur cette équation et chercher sur plusieurs forums. J'ai maintenant compris le raisonnement, merci à tous ceux qui m'ont aidé.
Re: (kx + 1)^2 - 8x = 0
non tu n'as pas cherché puisque tu n'as pas répondu aux questions posées sur l'autre forum ... ni suivi les conseils donnés ...
le pb n'est pas d'aller chercher une réponse ailleurs, le pb c'est de travailler !!!
le pb n'est pas d'aller chercher une réponse ailleurs, le pb c'est de travailler !!!
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: (kx + 1)^2 - 8x = 0
Dans un esprit visant à ménager la chèvre et le chou, je félicite lalia pour avoir maintenu sa recherche et sa demande jusqu'à obtenir en collaboration une réponse à son problème !
Les chemins menant à la compréhension "complète" d'un problème, d'un questionnement, sont différents d'une personne à une autre mais sont tous respectables... Nous n'avons pas tous la même vitesse d'acquisition (et heureusement quelque part pour la "vivabilité" du monde !) d'une information mais alors elle est remplacée par d'autres savoirs, perceptions, ... qui concourent à équilibrer le monde ... (je dévie dans le forum philo, dsl, mais ne dit-on pas que les maths et la philo c'est au fond la même chose !?...pour ma part j'en suis absolument convaincu !)
Les chemins menant à la compréhension "complète" d'un problème, d'un questionnement, sont différents d'une personne à une autre mais sont tous respectables... Nous n'avons pas tous la même vitesse d'acquisition (et heureusement quelque part pour la "vivabilité" du monde !) d'une information mais alors elle est remplacée par d'autres savoirs, perceptions, ... qui concourent à équilibrer le monde ... (je dévie dans le forum philo, dsl, mais ne dit-on pas que les maths et la philo c'est au fond la même chose !?...pour ma part j'en suis absolument convaincu !)
Modifié en dernier par laetidom le 21 Oct 2017, 21:47, modifié 2 fois.
Re: (kx + 1)^2 - 8x = 0
il n'y a pas à ménager la chèvre et le chou !!
1/ tu ne savais pas (autre fil sur autre forum) et évidemment je ne te le reproche pas ...
2/ tu as à nouveau donné trop de réponses
3/ il suffisait de répondre à
et tant qu'il ne saura pas répondre à ces deux questions élémentaires il ne saura pas faire de math ...
et ce n'est pas pour moi que je cause évidemment !!!
c'est dans l'intéret de l'apprenant qui veut réellement progresser !!!
1/ tu ne savais pas (autre fil sur autre forum) et évidemment je ne te le reproche pas ...
2/ tu as à nouveau donné trop de réponses
3/ il suffisait de répondre à
[/quote][quote=carpediem @ 19-10-2017 à 22:05]salut
charabia ...
1/ peux-tu développer et réduire correctement (le premeir membre de ) l'équation (kx + 1)^2 - 8x = 0 ?
2/ peux-tu calculer proprement le discriminant ?
et tant qu'il ne saura pas répondre à ces deux questions élémentaires il ne saura pas faire de math ...
et ce n'est pas pour moi que je cause évidemment !!!
c'est dans l'intéret de l'apprenant qui veut réellement progresser !!!
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: (kx + 1)^2 - 8x = 0
Pas de soucis zygomatique !,
Je comprends évidemment ta position, mais je sais que le monde a changé et alors "j'essaye" modestement "d'adapter" mon approche dans ce sens ... tout en sachant évidemment que je ne serais pas compris par tout le monde, il faut tout de même essayer d'avancer, de faire avancer ... et pourquoi pas aussi par la méthode douce !?... la méthode dure étant usée et sélective et non humaniste, en un mot systémique ! Si on veut que ce soit toujours le système qui gagne ! La loi du plus fort . . . mais le plus fort n'est pas forcément celui qu'on croit ... à méditer ...
. . .
[Je ne parle évidemment pas de lalia, je parle en général]
" Un sourire ne coûte rien à celui qui le donne mais peut faire tellement de bien à celui qui le reçoit ! " Je ne suis pas de ceux qui disent par exemple qu'un sourire ne s'entend pas au téléphone ! Et même par écrit, je suis sûr que ça se ressent...
Je comprends évidemment ta position, mais je sais que le monde a changé et alors "j'essaye" modestement "d'adapter" mon approche dans ce sens ... tout en sachant évidemment que je ne serais pas compris par tout le monde, il faut tout de même essayer d'avancer, de faire avancer ... et pourquoi pas aussi par la méthode douce !?... la méthode dure étant usée et sélective et non humaniste, en un mot systémique ! Si on veut que ce soit toujours le système qui gagne ! La loi du plus fort . . . mais le plus fort n'est pas forcément celui qu'on croit ... à méditer ...
. . .
n'est pas le 1er niveau des élèves en difficultés, il est déjà au 3ème ou 4ème rolon de l'échelle, mais moi je cherche à aider si je peux celui qui se trouve sur le 1er ! CELUI QUI EST TOUT EN BAS, celui-ci, soit on tente de le rattraper soit on le perd et il se dégouttera et ira à la console . . . alors que peut-être avec un mot, un sourire, une gentillesse, on aura pu le faire basculer du "bon" côté . . .zygomatique a écrit: l'apprenant qui veut réellement progresser !!!
[Je ne parle évidemment pas de lalia, je parle en général]
" Un sourire ne coûte rien à celui qui le donne mais peut faire tellement de bien à celui qui le reçoit ! " Je ne suis pas de ceux qui disent par exemple qu'un sourire ne s'entend pas au téléphone ! Et même par écrit, je suis sûr que ça se ressent...
Re: (kx + 1)^2 - 8x = 0
k=0 donne une équation à une et une seule solution.
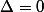 donne une équation à une solution double
donne une équation à une solution double
Re: (kx + 1)^2 - 8x = 0
mathelot a écrit:k=0 donne une équation à une et une seule solution.donne une équation à une solution double
En effet, autant être puriste !
Comme lalia parlait de k=2 je suis partis sur la solution double... mais peut-être qu'à la saisie de l'énoncé il y a eu une erreur d'appellation ...
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
