Pas compliqué
Olympiades mathématiques, énigmes et défis
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 14 Aoû 2017, 12:42
par MMu » 14 Aoû 2017, 12:42
Soient les réels positifs
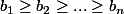
et
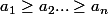
tels que

Montrer que
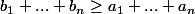


-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 14 Aoû 2017, 13:16
par zygomatique » 14 Aoû 2017, 13:16
salut
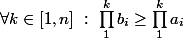
alors pour k = 1 :
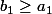
ensuite
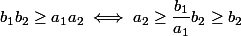
donc on peut réccurer
par conséquent
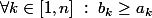
la conclusion est alors immédiate ...
merci ...

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 14 Aoû 2017, 15:17
par infernaleur » 14 Aoû 2017, 15:17
on est bien d'accord c'est a2<=b1*b2/a1 ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 14 Aoû 2017, 19:35
par zygomatique » 14 Aoû 2017, 19:35
ha merde ça marche plus ....

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
NumHéroBis
- Membre Naturel
- Messages: 20
- Enregistré le: 23 Juil 2017, 16:46
-
 par NumHéroBis » 15 Aoû 2017, 14:34
par NumHéroBis » 15 Aoû 2017, 14:34
Bonjour,
Je suppose tout d'abord que
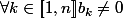
et de même pour les

car sinon il n'y a rien à prouver.
Soit P(n) :
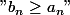
P(1) est vraie.
Supposons la vraie pour un certain
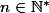
Alors
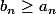
Supposons
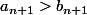
Alors,
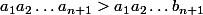
car les

sont positifs
Mais,
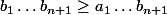
car
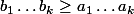
Donc,
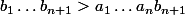
.
En divisant par
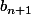
on obtient
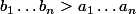
.
Il y a donc contradiction avec les hypothèse du début. On en conclut que
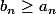
.
La proposition P(n) est alors vraie pour tout
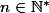
.
De ce fait,
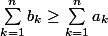
.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 15 Aoû 2017, 14:41
par infernaleur » 15 Aoû 2017, 14:41
où est la contradiction ??
-
NumHéroBis
- Membre Naturel
- Messages: 20
- Enregistré le: 23 Juil 2017, 16:46
-
 par NumHéroBis » 15 Aoû 2017, 14:43
par NumHéroBis » 15 Aoû 2017, 14:43
On avait supposé
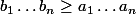
et l'on obtient
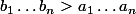
EDIT : En y réfléchissant il est vrai qu'il n'y a pas de contradiction à proprement parler. Cette démonstration est un peu bidon.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 15 Aoû 2017, 15:03
par infernaleur » 15 Aoû 2017, 15:03
et pour ta récurrence il aurait été préférable de supposer P(n-1) et démontrer P(n) car bn+1 et an+1 ne sont pas définis
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 03 Sep 2017, 09:57
par MMu » 03 Sep 2017, 09:57
Personne ?

-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 10 Sep 2017, 18:41
par MMu » 10 Sep 2017, 18:41
Do you know Karamata ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Sep 2017, 11:40
par Ben314 » 11 Sep 2017, 11:40
Avant, non (et j'arrivais péniblement à montrer le résultat via des disjonctions de cas pour n=4).
Maintenant..., oui :
Inégalité de Karamata a écrit:Si
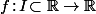
est convexe et que
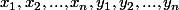
sont des éléments de

tels que :
(i)
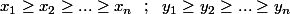
(ii)
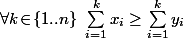
(iii)
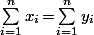 ou bien
ou bien 
est croissante sur

Alors
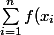\geq\sum_{i=1}^n f(y_i))
Modifié en dernier par
Ben314 le 11 Sep 2017, 11:58, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités


est convexe et que
sont des éléments de
tels que :
ou bien
est croissante sur