Bonjour,
Je bloque sur une question d'un devoir:
On note Qn(R) l'ensemble des matrices M de Mn(R) vérifiant sp(M)CU (U est l'ensemble des complexes de module 1) et det(M)=1
Montrer que si M est une matrice de Q2(R) n'admettant pas de valeur propre réelle, il existe P appartenant à GL2(R) et theta tels que P^-1MP=R
avec R la matrice (cos theta -sin theta
sin theta cos theta)
Auriez vous une idée sur le raisonnement à tenir?
Merci!
Diagonalisation
10 messages
- Page 1 sur 1
Salut,
Une piste : soit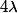 une des deux valeur propre (complexe) de M (l'autre est donc égale à ...)
une des deux valeur propre (complexe) de M (l'autre est donc égale à ...)
Comme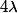 est de module égal à 1, il s'écrit
est de module égal à 1, il s'écrit 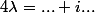 .
.
Soit un vecteur propre associé à
un vecteur propre associé à 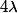 . On peut l'écrire
. On peut l'écrire 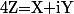 où
où  et le fait que
et le fait que 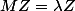 signifie que
signifie que =(...+i...)(X+iY)=\cdots) donc ...
donc ...
De plus, (X,Y) est une famille libre de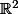 car sinon...
car sinon...
Une piste : soit
Comme
Soit
De plus, (X,Y) est une famille libre de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Salut,
Une piste : soitune des deux valeur propre (complexe) de M (l'autre est donc égale à ...)
Commeest de module égal à 1, il s'écrit
.
Soitun vecteur propre associé à
. On peut l'écrire
où
et le fait que
signifie que
donc ...
De plus, (X,Y) est une famille libre decar sinon...
La 2ème valeur propre est son conjugué, lambda peut s'écrire sous la forme: cos theta+isin theta
Chacune des valeurs propres est de multiplicité 1, la dimension de chaque espace propre associé est aussi 1.
Je cherche pour les autres implications.
Ben314 a écrit:Salut,
Une piste : soitune des deux valeur propre (complexe) de M (l'autre est donc égale à ...)
Commeest de module égal à 1, il s'écrit
.
Soitun vecteur propre associé à
. On peut l'écrire
où
et le fait que
signifie que
donc ...
De plus, (X,Y) est une famille libre decar sinon...
Je n'arrive pas à réécrire l'égalité MZ=lambdaZ, je ne vois pas comment écrire Z sous forme d'une matrice colonne...
Ben314 a écrit:Salut,
Une piste : soitune des deux valeur propre (complexe) de M (l'autre est donc égale à ...)
Commeest de module égal à 1, il s'écrit
.
Soitun vecteur propre associé à
. On peut l'écrire
où
et le fait que
signifie que
donc ...
De plus, (X,Y) est une famille libre decar sinon...
Alors j'obtiens que Z=0 ce qui est moyen pour un vecteur propre... :/
Le Z, le X et le Y dont je parle sont des vecteur colonne. Le Z est un vecteur colonne complexe et le X et le Y sont des vecteurs colonne réels.
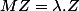 donne
donne 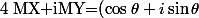(X+iY)=(\cos\theta X-\sin\theta Y)+i(\sin\theta X+\cos\theta Y))
Et comme un vecteur colonne complexe Z' s'écrit de façon unique sous la forme Z'=X'+iY' avec X' et Y' des vecteurs colonne réels, cela signifie que
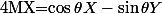 et
et 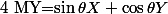 .
.
Donc une fois montré que (X,Y) est une base de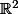 tu en déduira que l'endomorphisme de matrice M dans la base canonique a pour matrice ... dans la base (X,Y)
tu en déduira que l'endomorphisme de matrice M dans la base canonique a pour matrice ... dans la base (X,Y)
Et comme un vecteur colonne complexe Z' s'écrit de façon unique sous la forme Z'=X'+iY' avec X' et Y' des vecteurs colonne réels, cela signifie que
Donc une fois montré que (X,Y) est une base de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Le Z, le X et le Y dont je parle sont des vecteur colonne. Le Z est un vecteur colonne complexe et le X et le Y sont des vecteurs colonne réels.donne
Et comme un vecteur colonne complexe Z' s'écrit de façon unique sous la forme Z'=X'+iY' avec X' et Y' des vecteurs colonne réels, cela signifie queet
.
Donc une fois montré que (X,Y) est une base detu en déduira que l'endomorphisme de matrice M dans la base canonique a pour matrice ... dans la base (X,Y)
C'est bon je viens de comprendre!!!!! Merci beaucoup!!
Sujet réduction
Thildoucantal15 a écrit:Bonjour,
Je bloque sur une question d'un devoir:
On note Qn(R) l'ensemble des matrices M de Mn(R) vérifiant sp(M)CU (U est l'ensemble des complexes de module 1) et det(M)=1
Montrer que si M est une matrice de Q2(R) n'admettant pas de valeur propre réelle, il existe P appartenant à GL2(R) et theta tels que P^-1MP=R
avec R la matrice (cos theta -sin theta
sin theta cos theta)
Auriez vous une idée sur le raisonnement à tenir?
Merci!
Salut, pourrais tu me dire ton devoir était tiré de quel sujet stp?
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
