Calcul de limite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
campoke
- Messages: 5
- Enregistré le: 27 Oct 2015, 09:55
-
 par campoke » 27 Oct 2015, 10:06
par campoke » 27 Oct 2015, 10:06
Bonjour,
je dois trouver la limite de (a+sin(x))^x lorsque x tend vers +infini avec a>1
Je l'ai écrit sous la forme exponentielle mais je ne vois pas comment contourner l'indétermination de sin(x).Auriez-vous des pistes à me donner?
merci :)

-
WillyCagnes
- Membre Transcendant
- Messages: 3754
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 27 Oct 2015, 10:37
par WillyCagnes » 27 Oct 2015, 10:37
bjr
-1<= sin(x) <=1
-
campoke
- Messages: 5
- Enregistré le: 27 Oct 2015, 09:55
-
 par campoke » 27 Oct 2015, 10:56
par campoke » 27 Oct 2015, 10:56
merci,
du coup, on a+sin(x)>0 donc
pour les cas a>2 on trouve que (a+sinx)^x -> +infini
et pour les cas a<2 , a+sinx<1 donc (a+sinx)^x ->-0 ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 27 Oct 2015, 11:48
par zygomatique » 27 Oct 2015, 11:48
salut
puisque a > 1 et -1 =< sin x =< 1 prendre le logarithme ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
campoke
- Messages: 5
- Enregistré le: 27 Oct 2015, 09:55
-
 par campoke » 27 Oct 2015, 12:11
par campoke » 27 Oct 2015, 12:11
[quote="zygomatique"]salut
puisque a > 1 et -1 =1, ln(a+sinx)>ln(1) donc exp(x*ln(a+sinx))->+infini
a>2:
00
et pour le cas a=2 la limite existe-t-elle?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 27 Oct 2015, 13:28
par zygomatique » 27 Oct 2015, 13:28
campoke a écrit:merci

mais est-ce que que du coup on trouve une limite différente selon les valeurs de a?
avec a1, ln(a+sinx)>ln(1) donc exp(x*ln(a+sinx))->+infini
a>2:
00
et pour le cas a=2 la limite existe-t-elle?
) = xln(a) [1 + \dfrac {ln(1 + \dfrac {sin (x)}a)}{\ln a} ])
et |sin x|/a < 1 on peut faire une approximation affine
 \approx)
... ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 27 Oct 2015, 15:48
par Kolis » 27 Oct 2015, 15:48
Bonjour !
Si
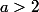
on a
>\ln(a-1)>0)
donc limite infinie.
Soit
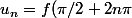=(a+1)^{\pi/2+2n\pi}=b(a+1)^{2n\pi})
: limite infinie
=(a-1)^{-\pi/2+2n\pi}=c(a-1)^{2n\pi})
Si

, la limite de

est nulle.
Si
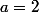
on a
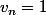
donc pour

,

n'a pas de limite en

-
lilou210
- Messages: 2
- Enregistré le: 03 Nov 2015, 19:44
-
 par lilou210 » 03 Nov 2015, 19:49
par lilou210 » 03 Nov 2015, 19:49
Bonjour, je suis bloquée sur un calcul de limite.
Calculer limite de exp(x^2.ln(2x)) en 0
Merci d'avance
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 04 Nov 2015, 08:18
par Kolis » 04 Nov 2015, 08:18
Bonjour !
Je crois qu'il vaut mieux éviter de squatter un fil ouvert par queslqu'un d'autre. Je te conseille d'ouvrir un fil personnel pour poser ta question !
-
tototo
- Membre Rationnel
- Messages: 954
- Enregistré le: 08 Nov 2011, 07:41
-
 par tototo » 04 Nov 2015, 13:16
par tototo » 04 Nov 2015, 13:16
Bonjour,
je dois trouver la limite de (a+sin(x))^x lorsque x tend vers +infini avec a>1
-12 la limite vaut + l'infini.
Je l'ai écrit sous la forme exponentielle mais je ne vois pas comment contourner l'indétermination de sin(x).Auriez-vous des pistes à me donner?
merci

[/quote]
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
