Bonjour à tous !
J'ai une question concernant un certain "type" de développement limité.
Je préfère donner des exemples:
* f(x) = x/(exp(x)-1)
* g(x) = 7x^3/(x-sin(x))
au voisinage de 0.
Le problème est que le dénominateur tend vers 0.
On peut diviser par le numérateur en haut et en bas:
f(x) = 1/((exp(x)-1)/x)
g(x) = 7/((x-sin(x))/x^3)
Mais pour appliquer toute formule du style: 1/(1+u) ou (1+u)^(-1) lorsque u tend vers 0 il faut mettre en évidence ce 1...
or il n'est pas évident dans les expressions de f et g
Du coup, l'astuce est de réinjecter le développement limité du dénominateur, avec le o(x^(...)), mais j'aimerais une technique un peu plus propre ?
J'espère que c'est assez clair, n'hésitez pas à me poser des questions sinon !
Développement limité
5 messages
- Page 1 sur 1
bjr
as tu vu en cours le developpement de fonction
f(x) = x/(exp(x)-1)
tu remplaces exp(x)=1+x+x²/2!+...
f(x) = x/(exp(x)-1)=x/[1 +x +x²/2+O(x) -1]
f(x)=x/(x+x²/2+...)
f(x)=1/(1+x/2+...)
qd x td vers 0 f(x) tend vers 1
tu peux utiliser la regle de l'Hôpital, en derivant le num et le denom de f(x)
1/exp(0)=1
http://limite.cours-de-math.eu/regle-hopital.php
2) developpe donc sin(x)=x/1 -x^3/3! +x^5/5! +O(x)
et continue la suite
as tu vu en cours le developpement de fonction
f(x) = x/(exp(x)-1)
tu remplaces exp(x)=1+x+x²/2!+...
f(x) = x/(exp(x)-1)=x/[1 +x +x²/2+O(x) -1]
f(x)=x/(x+x²/2+...)
f(x)=1/(1+x/2+...)
qd x td vers 0 f(x) tend vers 1
tu peux utiliser la regle de l'Hôpital, en derivant le num et le denom de f(x)
1/exp(0)=1
http://limite.cours-de-math.eu/regle-hopital.php
2) developpe donc sin(x)=x/1 -x^3/3! +x^5/5! +O(x)
et continue la suite
Bonjour... :happy:
Personnellement, je vois pas où est le problème en injectant le DL d'une fonction au sein d'une autre vu que l'on raisonne par équivalence en ce point...
Pour la fonction j'ai fait comme ça :
j'ai fait comme ça :
Soit la fonction telle que
telle que =\frac{x}{e^{x}-1}) ,
, 
En premier lieu, on injecte le DL de l'exponentielle et une fois que l'on peut, on applique le DL de avec un
avec un  tendant vers 0 en 0.
tendant vers 0 en 0.
:f(x)=\frac{x}{1+x+\frac{x^{2}}{2}+x^{2} \varepsilon_{1} (x)-1}=\frac{x}{x(1+\frac{x}{2}+x\varepsilon_{1}(x))}=\frac{1}{1+\frac{x}{2}+x\varepsilon_{1}(x)}=1-\frac{x}{2}+\frac{x^{2}}{4}+x^{2}\varepsilon_{2}(x))
avec=0) ,
, 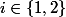
Je sais pas si ça te convient... :hein: Mais je ne vois pas de solution plus 'propre'...
Devancé par Willy... :langue:
Personnellement, je vois pas où est le problème en injectant le DL d'une fonction au sein d'une autre vu que l'on raisonne par équivalence en ce point...
Pour la fonction
Soit la fonction
En premier lieu, on injecte le DL de l'exponentielle et une fois que l'on peut, on applique le DL de
avec
Je sais pas si ça te convient... :hein: Mais je ne vois pas de solution plus 'propre'...
Devancé par Willy... :langue:
Merci beaucoup à vous deux, mais effectivement j'avais demandé une solution sans réinjecter de DL.
En fait, si je demande ça c'est parce que mon professeur était assez exigent sur les rédaction et n'aimait pas ce genre de chose même si c'est correct.
Il n'y a peut être pas d'autre manière alors... :/
En fait, si je demande ça c'est parce que mon professeur était assez exigent sur les rédaction et n'aimait pas ce genre de chose même si c'est correct.
Il n'y a peut être pas d'autre manière alors... :/
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
