Bonjour,
Je vais essayer d'être la plus claire possible. J'ai deux sommes. L'une allant de i=0 à i=k et l'autre allant de i=0 à i=100-k. Je voudrais trouver le k pour lequel le produit des deux sommes soit maximal. Le terme à l'intérieur des sommes n'est pas le même et il dépend de i et de k.
J'ai trouvé avec Maple le k qui me donne le produit le plus élevé mais je ne sais pas comment le prouver...
Merci
Maximiser le produit de deux sommes
5 messages
- Page 1 sur 1
Salut,
Pas super clair ton truc.... utilise MimeTeX.
Pour voir si je comprend : tu as deux suites_{0\leq i\leq 100}) et
et _{0\leq i\leq 100}) et tu voudrais savoir que est le
et tu voudrais savoir que est le  qui rend maximum
qui rend maximum 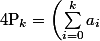\times\left(\sum_{i=0}^{100-k}b_i\right)) .
.
C'est ça ? Tes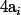 et
et  , ce sont des réels ? positifs ?
, ce sont des réels ? positifs ?
Pas super clair ton truc.... utilise MimeTeX.
Pour voir si je comprend : tu as deux suites
C'est ça ? Tes
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Salut,
Pas super clair ton truc.... utilise MimeTeX.
Pour voir si je comprend : tu as deux suites_{0\leq i\leq 100}) et
et _{0\leq i\leq 100}) et tu voudrais savoir que est le
et tu voudrais savoir que est le  qui rend maximum
qui rend maximum 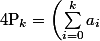\times\left(\sum_{i=0}^{100-k}b_i\right)) .
.
C'est ça ? Tes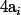 et
et  , ce sont des réels ? positifs ? connus ? ayant certaines propriétés ?
, ce sont des réels ? positifs ? connus ? ayant certaines propriétés ?
Pas super clair ton truc.... utilise MimeTeX.
Pour voir si je comprend : tu as deux suites
C'est ça ? Tes
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Dans ce cas, vu que c'est des suites géométriques, on a trivialement la valeur des différents Pk et on se fout comme de l'an 40 de savoir que le Pk en question provient d'un produit de somme de trucs :
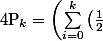^i\right) \times \left(\sum_{i=0}^{100-k}2^{i-2k-1\right) <br />= \frac{1-\left(\frac{1}{2}\right)^{k+1}} {1-\frac{1}{2}\ \ \ } \times 2^{-2k-1} \times \frac{1-2^{100-k+1}}{1-2\ \ \ }<br />= \left(1-\frac{1}{2}X\right)X^2\left(2^{101}X-1\right)<br />=F(X)\) où
où 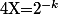
et tu t'en sort facilement en étudiant les variations de F.
et tu t'en sort facilement en étudiant les variations de F.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 98 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
