Bonjour, à toutes à tous j'ai un DM à faire en maths je suis en 1ere année de licence c'est une chance pour moi de pouvoir me rattraper je ne suis pas la pour vous demandez les réponses sa ne servirais à rien je veux seulement que vous puissiez m'expliquez si vous le pouvez le raisonnement à suivre pour réaliser mes exercices correctement. Si vous avez des exemples ou des schemas sa serais vraiment le top je vous remercie
Je dois faire l'exo 10 (1), l'exo 11 (3), l'exo 12 (3) et l'exo 15.
Lien du PDF : http://www.docdroid.net/wr0a/planche-5.pdf.html
Ce que j'ai déjà compris c'est qu'il faut déjà trouver la partie Réelle pour ensuite utiliser le Theoreme de Taylor ?
Cordialement, Ben.
Développement limité
13 messages
- Page 1 sur 1
par zygomatique » 07 Avr 2015, 19:05
salut
ex 10 ::
1/ si f admet un dl alors sa primitive avec la bonne constante d'intégration admet un dl par primitivation du dl de f ...
si f admet un dl en 0 alors
admet un dl (par composition) ...
ex 10 ::
1/ si f admet un dl alors sa primitive avec la bonne constante d'intégration admet un dl par primitivation du dl de f ...
si f admet un dl en 0 alors
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
par mathelot » 08 Avr 2015, 09:09
méthodes pratiques:
Un DL en
peut se dériver ou peut s'intégrer
Les DL peuvent se composer
exemple: on pose
Les fonctions paires (resp. impaires) admettent des DL pairs (resp. impairs)
les fonctions de classe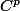
admettent des DL à l'ordre 
(la réciproque étant fausse)
le DL de^{\alpha})
est une généralisation de la formule du binome
aux valeurs de
non entières
Un DL en
Les DL peuvent se composer
exemple: on pose
Les fonctions paires (resp. impaires) admettent des DL pairs (resp. impairs)
les fonctions de classe
(la réciproque étant fausse)
le DL de
aux valeurs de
par Ben314 » 08 Avr 2015, 09:27
non, pas sans hypothèses supplémentairesmathelot a écrit:Un DL en
Par exemple,
admet un D.L. (trivial) à l'ordre n-1 en 0
alors que f' n'admet même pas un D.L. à l'ordre 0 vu qu'elle n'est pas continue en 0.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par mathelot » 08 Avr 2015, 09:43
oui, il y a deux types d'études pour les DL
Dans le premier type, on suppose que les fonctions f,f',f'', etc..
admettent des développements de Taylor, Taylor Lagrange, Taylor-Young ou reste intégral,
si f est de classe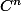
Dans le second type , f est définie par son DL(0) et là, il peut y avoir
de la pathologie car l'existence d'un DL en x=0 n'entraine pas la dérivabilité
de f dans un voisinage ouvert de zéro
Dans le premier type, on suppose que les fonctions f,f',f'', etc..
admettent des développements de Taylor, Taylor Lagrange, Taylor-Young ou reste intégral,
si f est de classe
Dans le second type , f est définie par son DL(0) et là, il peut y avoir
de la pathologie car l'existence d'un DL en x=0 n'entraine pas la dérivabilité
de f dans un voisinage ouvert de zéro
par mathelot » 08 Avr 2015, 14:15
supposons f de classe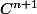 
dans un voisinage de a.
en intégrant par parties
=f(a)+\frac{(x-a)}{1!}f'(a)+\frac{(x-a)^2}{2!}f''(a)+...+\frac{(x-a)^n}{n!}f^{(n)}(a)+\int_{a}^{x} \, \frac{(x-t)^n}{n!} f^{(n+1)}(t) dt)
Comme voisinage K, on prend un intervalle compact d'intérieur non vide contenant a
(la connexité pour intégrer, la compacité pour majorer}|)
)
si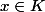
^n}{n!} f^{(n+1)}(t) dt=o((x-a)^n))
en appliquant à
la classe 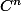, on voit que le DL(a)
de f' est la dérivée (sans évoquer le reste) du DL(a) de f.
en intégrant par parties
Comme voisinage K, on prend un intervalle compact d'intérieur non vide contenant a
(la connexité pour intégrer, la compacité pour majorer
si
en appliquant à
de f' est la dérivée (sans évoquer le reste) du DL(a) de f.
par Ben314 » 08 Avr 2015, 15:11
Oui, mais d'un autre coté, si tu suppose f de classe C^n, il n'y a absolument rien à démontrer vu que dans ce cas, la formule de Taylors te donne le D.L. de f, à savoir :
=f(a)+\frac{(x-a)}{1!}f'(a)+\frac{(x-a)^2}{2!}f''(a)+...+\frac{(x-a)^n}{n!}f^{(n)}(a)+o((x-a)^n))
mais que cette même formule, appliquée à f' (on peut car f' est par hypothèse de classe C^(n-1) ) donne
=f'(a)+\frac{(x-a)}{1!}f''(a)+\frac{(x-a)^2}{2!}f'''(a)+...+\frac{(x-a)^{n-1}}{(n-1)!}f^{(n)}(a)+o((x-a)^{n-1}))
donc il y a juste a "regarder" les deux formules pour vérifier que l'on passe de la première à la deuxième en dérivant les trucs devant le o(?)
Donc zéro calcul à faire dans ce cas.
En fait, c'est la même chose dans tout les cas où on met dans les hypothèse le fait que "f est de classe C^n" mais ce sont des hypothèses bien trop restrictives pour beaucoup de cas où on a affaire à des fonction de la forme f(x)=g(x)/h(x) qui sont des formes indéterminés lorsque x->0 (donc rien que la continuité de f en 0 n'est pas du tout évidente alors qu'on veut un D.L. à l'ordre 5 ou 6 de f...)
mais que cette même formule, appliquée à f' (on peut car f' est par hypothèse de classe C^(n-1) ) donne
donc il y a juste a "regarder" les deux formules pour vérifier que l'on passe de la première à la deuxième en dérivant les trucs devant le o(?)
Donc zéro calcul à faire dans ce cas.
En fait, c'est la même chose dans tout les cas où on met dans les hypothèse le fait que "f est de classe C^n" mais ce sont des hypothèses bien trop restrictives pour beaucoup de cas où on a affaire à des fonction de la forme f(x)=g(x)/h(x) qui sont des formes indéterminés lorsque x->0 (donc rien que la continuité de f en 0 n'est pas du tout évidente alors qu'on veut un D.L. à l'ordre 5 ou 6 de f...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 08 Avr 2015, 15:27
Un peu comme si c'était de la forme =\int_{a(x)}^{b(x)}\varphi(x,t)dt)
qui, avec les bonnes hypothèses sur 
se dérive en =b'(x)\varphi(x,b(x))-a'(x)\varphi(x,a(x))+\int_{a(x)}^{b(x)} \frac{ \partial \varphi}{ \partial x}(x,t)dt)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 08 Avr 2015, 16:33
Avec les bonnes hypothèses de régularité,
=\int_{a(x)}^{b(x)}\varphi(x,t)dt\ =\ \psi\big(x,b(x)\big)-\psi\big(x,a(x)\big)\)
où 
est telle que 
.
En utilisant la dérivation pour les fonction composées (de 2 variables), il vient :
\ =\ \frac{\partial \psi}{\partial x}\big(x,b(x)\big)+b'(x)\frac{\partial \psi}{\partial t}\big(x,b(x)\big)-\frac{\partial \psi}{\partial x}\big(x,a(x)\big)-a'(x)\frac{\partial \psi}{\partial t}\big(x,a(x)\big))
\varphi\big(x,b(x)\big)-a'(x)\varphi\big(x,a(x)\big)<br />+ \int_{a(x)}^{b(x)}\frac{\partial^2 \psi}{\partial t\partial x}(x,t)dt)
\varphi\big(x,b(x)\big)-a'(x)\varphi\big(x,a(x)\big)<br />+ \int_{a(x)}^{b(x)}\frac{\partial \varphi}{\partial x}(x,t)dt\ \ \ \ \)
(Schwarz)
En utilisant la dérivation pour les fonction composées (de 2 variables), il vient :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :