Système d'équation dans IR²
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dionus
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Jan 2015, 00:06
-
 par Dionus » 07 Mar 2015, 21:27
par Dionus » 07 Mar 2015, 21:27
Bonsoir j'ai un problème avec un système d'équations :

Je ne connais que le genre

où on utilise Somme et Produit pour résoudre
-
mathelot
 par mathelot » 07 Mar 2015, 21:30
par mathelot » 07 Mar 2015, 21:30
bonjour,
développe
^3)
et remplace ce que tu peux par les valeurs.
sinon (2;-1) est solution évidente

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 08 Mar 2015, 09:26
par chan79 » 08 Mar 2015, 09:26
salut
ou alors
x³+y³=(x+y)(x²-xy+y²)
7=x²-xy+y²
7=x²-x(1-x)+(1-x)²
7=3x²-3x+1
x²-x-2=0
(x+1)(x-2)=0
deux solutions:
(-1,2) (2,-1)
Ce sont des équations et non des inéquations :zen:
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 08 Mar 2015, 09:29
par nodjim » 08 Mar 2015, 09:29
Dionus, c'est un système d'équations, pas d'inéquations. Le titre doit, dans la mesure du possible, être en adéquation avec le problème posé.
-
Dionus
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Jan 2015, 00:06
-
 par Dionus » 08 Mar 2015, 10:21
par Dionus » 08 Mar 2015, 10:21
chan79 a écrit:salut
ou alors
x³+y³=(x+y)(x²-xy+y²)
7=x²-xy+y²
7=x²-x(1-x)+(1-x)²
7=3x²-3x+1
x²-x-2=0
(x+1)(x-2)=0
deux solutions:
(-1,2) (2,-1)
Ce sont des équations et non des inéquations :zen:
J'ai corrigé mon erreur dans le titre désolé. Et euh sinon je comprend pas que de (x+y)(x²-xy+y²) tu obtiennes 7=x²-xy+y² parce que ici (x+y) est en facteur et tu l'a remplacé par 7 ce qui donne 7(x²-xy+y²) ensuite tu transpose le 7 et comme il multipliait si on le transpose il divise ce qui donne normalement 1/7=x²-xy+y² et puis ici 7=x²-x(1-x)+(1-x)² ou est passé le y?
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 08 Mar 2015, 10:57
par nodjim » 08 Mar 2015, 10:57
Peut être plus simple:
y=1-x
x^3+y^3=x^3+(1-x)^3=7
le terme en x^3 disparait après développement et ne reste qu'un facile second degré.
-
Dionus
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Jan 2015, 00:06
-
 par Dionus » 08 Mar 2015, 12:23
par Dionus » 08 Mar 2015, 12:23
nodjim a écrit:Peut être plus simple:
y=1-x
x^3+y^3=x^3+(1-x)^3=7
le terme en x^3 disparait après développement et ne reste qu'un facile second degré.
Je comprends un peu mieux j'ai remplacé y=1-x et (x+y) par sa valeur 1 puis j'ai développé ça m'a bel est bien donné 7=3x²-3x+1 mais j'ai pas compris que il est passé de 7=3x²-3x+1
x²-x-2=0
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 08 Mar 2015, 12:37
par nodjim » 08 Mar 2015, 12:37
3x²-3x+1=7
3x²-3x+1-7=0
3x²-3x-6=0
3(x²-x-2)=0
x²-x-2=0

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 08 Mar 2015, 12:38
par chan79 » 08 Mar 2015, 12:38
Dionus a écrit:Je comprends un peu mieux j'ai remplacé y=1-x et (x+y) par sa valeur 1 puis j'ai développé ça m'a bel est bien donné 7=3x²-3x+1 mais j'ai pas compris que il est passé de 7=3x²-3x+1
x²-x-2=0
7=3x²-3x+1
0=3x²-3x+1-7
0=3x²-3x-6
3(x²-x-2)=0
x²-x-2=0
-
Dionus
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Jan 2015, 00:06
-
 par Dionus » 08 Mar 2015, 13:39
par Dionus » 08 Mar 2015, 13:39
chan79 a écrit:7=3x²-3x+1
0=3x²-3x+1-7
0=3x²-3x-6
3(x²-x-2)=0
x²-x-2=0
:mur: après avoir calculé ça -1 est racine évidente à partir de là on factorise (x+1)(x-2)=0 on obtient x1=-1 et x2=2 maintenant je me demandais comment formuler tout le processus (je dois corriger l'exercice au tableau et expliquer le cheminement d'ou les précisions que j'ai demandées) je propose :

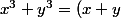(x^2-xy+y^2))
or

et
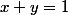
donc je les remplace par leur valeur et ça donne

puis dans
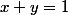
on a
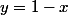
donc je remplace y par sa valeur dans

ce qui donne
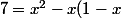+(1-x)^2)
en développant ça donne

puis je transpose le

ça donne

je mets

en facteur puis je le transpose le

l'élimine et j'obtiens
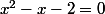
,

est racine évidente à partir de là on factorise l'équation et on a
(x-2)=0)
on obtient
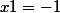
et
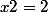
les couples
)
et
)
vérifient le système alors
;(2;-1)\end{array}<br />\right)
qu'en pensez vous?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités