Compte est bon ?

[Buridan]

Bonjour,
Il faut trouver 2000 avec tous les chiffres de 0 à 9, utilisés une seule fois et seule l'addition est autorisée. On a le droit de former un nombre avec plusieurs chiffres: 29, 804, 1356...

Problème posé en primaire. :doh:

[Buridan]

Bonjour,
Il faut trouver 2000 avec tous les chiffres de 0 à 9, utilisés une seule fois et seule l'addition est autorisée. On a le droit de former un nombre avec plusieurs chiffres: 29, 804, 1356...

Problème posé en primaire. :doh:

Ce que je pensais au départ comme une énigme facile ne l'est pas finalement, est-ce possible au moins ?

[nodjim]

Pour un niveau collège, c'est assez difficile. Pour du primaire, l'instit. doit vouloir tester les parents... On peut prouver que c'est impossible en remarquant que la somme des chiffres vaut 45 et en établissant une somme "à trous" dont le résultat est 2000. La somme des unités doit faire 10 ou 20 (au dela c'est impossible), la somme des dizaines aussi, la somme des centaines aussi. Les cas possibles à examiner, en partant de ces contraintes, ne sont pas nombreux. Penser tout de même aux retenues.

[mathelot]

j'essaye avec le complément à 9 qui est bien injectif
0-9 1-8 2-7 3-6 4-5

je me demande s'il y a une solution car en ajoutant les chiffres
de 0 à 9


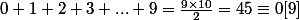
tandis que

est ce que ceci démontre qu'il n'y a pas de solution ?

[nodjim]

Oui c'est bon, mathelot ! Modulo 9, la position d'un chiffre dans le nombre ne change pas sa valeur modulo 9. C'est donc comme si on les mettait tous dans la colonne unité.
Je me souviens de la preuve par 9 dans les mutilplications en primaire, mais c'était le seul usage qu'on savait faire.

[mathelot]

on pourrait essayer avec 2016, ça nous laisse un an pour réfléchir

[chan79]

on pourrait essayer avec 2016, ça nous laisse un an pour réfléchir

Il doit y avoir pas mal de solutions
On peut les trouver avec un petit programme mais est-ce que ça vaut le coup ?
Sans programmer, on peut en trouver assez facilement certaines du genre:
1978+20+3+4+5+6=2016
1970+23+4+5+6+8=2016
1960+34+2+5+7+8=2016
1950+46+2+3+7+8=2016
1940+7+8+56+2+3=2016
1930+67+2+4+5+8=2016
1920+73+4+5+6+8=2016

[chan79]

En fait, pour ce format **** + ** + * + * + * + * =2016
il y a ces trois solutions:

1920+73+4+5+6+8=2016
1930+62+4+5+7+8=2016
1940+52+3+6+7+8=2016

A partir de là, on peut faire certaines permutations des chiffres des unités ou des dizaines.(deux positions possibles pour 0)
soit en tout 1440 solutions pour ce format (à vérifier s'il y a des amateurs)

[nodjim]

Rien sur le format ****+***+*** ?

[chan79]

Rien sur le format ****+***+*** ?

En voilà un
1034+285+697=2016

également

1840+72+93+5+6=2016
201+834+975+6=2016

[nodjim]

Bravo chan