Besoin d'explications ( vecteurs )

[Kimberley123]

Alors lundi j'ai un ds sur le calcul vectorielle et je ne conprends absolument rien et ce même en relisant plusieurs fois mon cours. Quelqu'un pourrait donc m'expliquer CLAIREMENTcomment montrer que trois points sont alignés avec un réel k ?

[Sylviel]

Il faudrait un peu plus de contexte a ta question...

J'essaie une reponse. pose des questions de la ou tu ne comprends pas.

Trois point A,B,C sont alignes si et seulement si
les vecteurs et 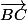sont colineaires.
Cela signifie que l'un est egal a k fois l'autre (peu importe le k).

En pratique :
1) calculer les coordonnees de et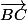




2) calculer un k possible :
si k existe alors
3) verifier si k est bon :
verifier que , si ce n'est pas le cas les points ne sont pas alignes


Exemple :
A(1,2) B(2,4) C(4,8)




on pose

et on a bien


:zen:

[mathelot]

ou


=det(u;v)

si det =0 les vecteurs sont liés et les bi-points indiquent la même direction

si det 0 les points ne sont pas alignés

[Sylviel]

Es-tu sur que le determinant est au programme du lycee ?

[mathelot]

Es-tu sur que le determinant est au programme du lycee ?

Quelques élèves de Seconde connaissent (à vérifier toutefois).






si , en supposant les vecteurs non nuls:

par exemple, x 0







les vecteurs étant proportionnels, c'est la condition d'alignement des points A,B,C

[mathelot]

En pratique,pour deux vecteurs non nuls,

tu calcules le coefficient de proportionnalité.

puis tu calcules . si ce dernier quotient vaut k,
les points sont alignés sinon, ils ne sont pas alignés

[Kimberley123]

Merci à tous pour vos réponses ! Je commence à mieux comprendre.

[Kimberley123]

ou


=det(u;v)

si det =0 les vecteurs sont liés et les bi-points indiquent la même direction

si det 0 les points ne sont pas alignés

Bonjour ! Je n'ai pas vu cette notion :/

[Kimberley123]

Il faudrait un peu plus de contexte a ta question...

J'essaie une reponse. pose des questions de la ou tu ne comprends pas.

Trois point A,B,C sont alignes si et seulement si
les vecteurs et sont colineaires.
Cela signifie que l'un est egal a k fois l'autre (peu importe le k).

En pratique :
1) calculer les coordonnees de et




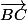
2) calculer un k possible :
si k existe alors
3) verifier si k est bon :
verifier que , si ce n'est pas le cas les points ne sont pas alignes


Exemple :
A(1,2) B(2,4) C(4,8)




on pose

et on a bien


:zen:

Bonjour ! Merci beaucoup ta réponse m'a bien aidée néanmoins je ne comprends pas la notion de multiplier un vecteur par un réel. Par exemple je ne comprends pas la consigne suivante:

A, B deux points du plan. Soit I le milieu de [AB]. Montree que le vecteur AI= 1/2.vecteur AB :/

[Math3matiqu3]

Bonjour ! Merci beaucoup ta réponse m'a bien aidée néanmoins je ne comprends pas la notion de multiplier un vecteur par un réel. Par exemple je ne comprends pas la consigne suivante:

A, B deux points du plan. Soit I le milieu de [AB]. Montree que le vecteur AI= 1/2.vecteur AB :/

Bonjour,

si I le milieu de [AB] , on est d'accord que AI + IB = AB (relation de chale) et que AI = IB donc 2AI = AB

soit AI = AB/2 donc AI = 1/2 AB

[mathelot]

Bonjour,

si I le milieu de [AB] , on est d'accord que AI + IB = AB (relation de Chasles) et que AI = IB donc 2AI = AB

soit AI = AB/2 donc AI = 1/2 AB

..........................................

Par contre , si les bi-points et sont colinéaires (proportionnels)
ça ne donne que le parallèlisme des deux droites (et si les droites sont les mêmes,
auquel cas les points sont alignés, c'est un cas particulier de parallèlisme)

[Math3matiqu3]

..........................................

Par contre , si les bi-points et sont colinéaires (proportionnels)
ça ne donne que le parallèlisme des deux droites (et si les droites sont les mêmes,
auquel cas les points sont alignés, c'est un cas particulier de parallèlisme)

Effectivement !