Lipshtz
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 10 Jan 2015, 10:30
par adamNIDO » 10 Jan 2015, 10:30
Bonjour,

merci pour votre aide
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 10 Jan 2015, 20:02
par adamNIDO » 10 Jan 2015, 20:02
Bonjour,
personne :hein:
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 11 Jan 2015, 10:39
par adamNIDO » 11 Jan 2015, 10:39
voila si je me rappel bien la defintion d'une app lipschitzienne
Soient E une partie de

, f:E;)R une application et k un réel positif.
On dit que

est k-lipschitzienne si
\in E^2,~|f(x)-f(y)|\le k~|x-y|.)
Donc on doit montrer :
\in R^2,~|\varphi(x)-\varphi(y)|\le k~|x-y|.)

et

étant supposées bornées alors il existe un réel

tel que

on ait
| \leq M)
et
| \leq M)
.
Soient

.
.Soit

.
On a :
 + u.g(x) = f(x) + v.g(x) + (u -v)g(x)\leq \varphi(v) + |u -v|.M)
Comment je peux passer au sup pour dire que .
\leq \varphi(v) + |u-v|.M)
.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 11 Jan 2015, 13:06
par adamNIDO » 11 Jan 2015, 13:06
Bonjour,
aucune aide
-
Wataru
- Membre Naturel
- Messages: 24
- Enregistré le: 29 Aoû 2014, 16:11
-
 par Wataru » 11 Jan 2015, 14:18
par Wataru » 11 Jan 2015, 14:18
Salut,
Bornées sur un compact.
-
mathelot
 par mathelot » 11 Jan 2015, 14:41
par mathelot » 11 Jan 2015, 14:41

est bornée sur le compact (0,1) mais pas Lipschitz
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 11 Jan 2015, 15:37
par adamNIDO » 11 Jan 2015, 15:37
mathelot a écrit:
est bornée sur le compact (0,1) mais pas Lipschitz
alors quoi faire monsieur pour justifie le passage a sup
-
mathelot
 par mathelot » 11 Jan 2015, 16:11
par mathelot » 11 Jan 2015, 16:11
je ne sais pas faire.
pour 'instant, j'ai remplacé les sup par des max,
supposées f,g continues et songé à
|d|=max(d,-d)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 11 Jan 2015, 16:43
par zygomatique » 11 Jan 2015, 16:43
salut
 = Sup_{x \in [0, 1]} \{f(x) + ug(x)\})
 = Sup_{y \in [0, 1]} \{f(y) + vg(y)\})
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 11 Jan 2015, 17:14
par zygomatique » 11 Jan 2015, 17:14
salut
 = Sup_{x \in [0, 1]} \{f(x) + ug(x)\})
 = Sup_{y \in [0, 1]} \{f(y) + vg(y)\})
soit e > 0
il existe a et b dans [0, 1] tels que |F(u) - f(a) - ug(a)| < e et |F(v) - f(b) - vg(b)| < e (par définition du sup)
donc
-e < F(u) - f(a) - ug(a) < e
-e < f(b) + vg(b) - F(v) < e
-2e < F(u) - F(v) + f(b) - f(a) + vg(b) - ug(a) < 2e
ouais .... bof .... faudrait arriver à a = b ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 11 Jan 2015, 18:36
par adamNIDO » 11 Jan 2015, 18:36
mathelot a écrit:je ne sais pas faire.
pour 'instant, j'ai remplacé les sup par des max,
supposées f,g continues et songé à
|d|=max(d,-d)
+u\ g(x) \le (f(x)+v\ g(x))+M|u-v| \le \varphi(v)+M|u-v|\quad (1))
la formule de 1 est dit que le nombre
+M|u-v|)
est un majorant pour l'ensemble
+u\ g(x):x\in[0,1]\})
.
par definition de sup on a :
\le \varphi(v)+M|u-v| \quad (2))
on reprend ce qu'on a fait precedement
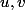
interchangés pour obtenir
\le \varphi(u)+M|u-v| \quad (3))
Finalement, combine (2) et (3) pour avoir
- \varphi(v)|\le M|u-v| \quad 4)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 11 Jan 2015, 18:50
par zygomatique » 11 Jan 2015, 18:50
pourquoi serait-ce le même x qui donne le sup pour u et pour v ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Wataru
- Membre Naturel
- Messages: 24
- Enregistré le: 29 Aoû 2014, 16:11
-
 par Wataru » 11 Jan 2015, 19:38
par Wataru » 11 Jan 2015, 19:38
J'ai pas vraiment compris mathelot, si tu parlais à moi ou pas xD...
J'avais lancé le borné sur un compact pour changer le sup en max, c'était pas pour justifier le caractère lipschitzien de la fonction :D
J'sais pas comment faire, j'ai pas vraiment réfléchi plus... Mais je me dis que considérer un seul M pour les deux fonctions c'est pas forcément le mieux à faire. Moi je prendrais un M comme borne de f et un M' comme borne de g. Parce qu'avec le f + ug, en considérant un seul M pour les deux on a du (M+1)u ce qui est embêtant pour la différence alors qu'avec M + M'*u, avec un peu de chance les M se simplifieront.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 11 Jan 2015, 20:02
par adamNIDO » 11 Jan 2015, 20:02
zygomatique a écrit:pourquoi serait-ce le même x qui donne le sup pour u et pour v ...
personne ne dit la même x donnerait sup pour u et v.
-
mathelot
 par mathelot » 12 Jan 2015, 12:58
par mathelot » 12 Jan 2015, 12:58
Wataru a écrit:J'ai pas vraiment compris mathelot, si tu parlais à moi ou pas xD...
J'avais lancé le borné sur un compact pour changer le sup en max
ah oui d'acccord
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
