Développement limité 2

[Poulimi]

Alors pour la dernière, franchement je ne suis vraiment pas sur j'ai utilisé les équivalents mais c'est quelque chose que je ne maîtrise pas bien du tout... Donc voilà mon expression de base
J'ai (xln(x)-xln(x+2))=xln((x)/(x+2)) car ln(a)-ln(b) =ln(a/b)
comme x/(x+2) peut aussi s'écrire sous la forme (x-2+2)/(x+2)=1-(2/(x+2)) mon expression devient donc xln(1- (2/x+2)) or ln(1+u) équivalent à u

mon expression est donc - 2x/(x+2) en +OO cela tend vers -2 voilà je ne sais pas trop

[deltab]

Alors pour la dernière, franchement je ne suis vraiment pas sur j'ai utilisé les équivalents mais c'est quelque chose que je ne maîtrise pas bien du tout... Donc voilà mon expression de base
J'ai (xln(x)-xln(x+2))=xln((x)/(x+2)) car ln(a)-ln(b) =ln(a/b)
comme x/(x+2) peut aussi s'écrire sous la forme (x-2+2)/(x+2)=1-(2/(x+2)) mon expression devient donc xln(1- (2/x+2)) or ln(1+u) équivalent à u

mon expression est donc - 2x/(x+2) en +OO cela tend vers -2 voilà je ne sais pas trop

Ok pour le résultat
ou encore sous la forme

Pour la règle de L'Hôpital, c'est bon.
Relis mon précédent message je l'avait modifié entre temps

[Poulimi]

Ok pour le résultat
ou encore sous la forme

Pour la règle de L'Hôpital, c'est bon.
Relis mon précédent message je l'avait modifié entre temps

Ok normalement c'est bon
donc après factorisation du polynôme et j'oublie ce que j'avais fait avec le conjugué j'obtiens
(x²-1)ln(x+1)+(x²-1)ln(7x²-3x+3)=(x-1)(x+1)ln(x+1)+(x-1)(x+1)ln(7x²-3x+3)
en posant t=x+1 on a t qui tend vers 0 si x tend vers -1
j'obtiens donc (t-2)tln(t)+(t-2)tln(7(t-1)²-3(t-1)+3)=(t-2)tln(t)+(t-2)tln(7t²-17t+13) en 0 tout cela tend vers 0 c'est bon ? Mais j'ai quand même l'impression de m'être compliqué la vie avec la factorisation du polynôme de degré 3 du coup ça m'a obligé à faire une résolution d'équation par identification... Il n'y avait pas une méthode plus simple
En tout cas merci pour ton aide il m'en reste une dernière à faire je vais essayer de la chercher

[deltab]

Mais j'ai quand même l'impression de m'être compliqué la vie avec la factorisation du polynôme de degré 3 du coup ça m'a obligé à faire une résolution d'équation par identification... Il n'y avait pas une méthode plus simple.

Il est inutile d'appliquer le changement de variable au facteur x-1, il ne pose pas de problème, sa limite est -2
Si. En écrivant , et calculer la limite de chaque crochet, la premier par la règle de L'Hôpiltal , le 2ème a été ramené à la forme qund
Je me base sur que tu fais pour te guider. De plus on ne trouve pas la meilleure réponse du 1er coup.
Pour l'avant-dernière, prend son log et essaies d'avoir la forme avec tendant vers (Ici est fonction rationnelle de x de même pour ).

[Poulimi]

Il est inutile d'appliquer le changement de variable au facteur x-1, il ne pose pas de problème, sa limite est -2
Si. En écrivant , et calculer la limite de chaque crochet, la premier par la règle de L'Hôpiltal , le 2ème a été ramené à la forme qund
Je me base sur que tu fais pour te guider. De plus on ne trouve pas la meilleure réponse du 1er coup.
Pour l'avant-dernière, prend son log et essaies d'avoir la forme avec tendant vers (Ici est fonction rationnelle de x de même pour ).

hum... ok mais en fait il y quelque chose que je ne comprends pas concernant la limite avec le polynôme de degré 3. Si j'applique le changement de variable au deuxième crochet je dois le faire aussi au premier ou pas la peine ? Parce que du coup c'est un peu confus dans ma tête avec ce que j'ai fait car je pensais que si j'appliquais un changement de variable j'étais obligé de le faire pour toute l'expression c'est pour ça en fait que quand j'ai posé t=x+1 j'avais du coup transformé (x-1) en (t-2). Pour l'avant dernière je compte faire a^b =exp(bln(a)) je vais quelque part en faisant ça ?
Merci pour l'astuce plus simple concernant le polynôme de degré 3

[deltab]

hum... ok mais en fait il y quelque chose que je ne comprends pas concernant la limite avec le polynôme de degré 3. Si j'applique le changement de variable au deuxième crochet je dois le faire aussi au premier ou pas la peine ? Parce que du coup c'est un peu confus dans ma tête avec ce que j'ai fait car je pensais que si j'appliquais un changement de variable j'étais obligé de le faire pour toute l'expression c'est pour ça en fait que quand j'ai posé t=x+1 j'avais du coup transformé (x-1) en (t-2). Pour l'avant dernière je compte faire a^b =exp(bln(a)) je vais quelque part en faisant ça ?
Merci pour l'astuce plus simple concernant le polynôme de degré 3

Pas la peine! Dans le calcul de la limite d'un produit de facteurs, certains facteurs peuvent être regroupés et calculer séparément la limite de chaque facteur. Si tous les facteurs admettent une limite finie, leur produit aussi. Que suffit-il d'avoir pour conclure si un ou plusieurs tendent vers ou -
Pour l'avant dernière je compte faire a^b =exp(bln(a)),
Ce que j'ai proposé revient au même mais évite de trainer à chaque fois l'exponentielle.
PS.
Qu'aurais tu fait pour où et sont des polynômes s'annulant en
A + dans la journée.

[deltab]

Bonjour.

La forme que j'ai donnée pour l'avant dernière limite est erronée mais essaies de t'en inspirer.

[Mikihisa]

La fonction f définie par

Si a!=0

Alors la fonction tend vers +oo si a>0 et vers 0 si a0 et vers 0 si b<0.

Ça se démontre assez facilement, il suffit d'avoir montrer que ln x/x tend vers 0, puis de transformer un peu l'expression.

Tu peux ajouter l'équivalence des polynome avec leurs terme de plus haut degré en l'infini.
En composant tout ça puis en jouant sur les facteur tu te ramène a des expression de la forme quenj´ai énoncé plus haut.

[deltab]

Salut Mikihisa.
Je suppose que a, b et c sont des constantes. Si ta remarque concerne l'avant dernière limite, es-tu sure qu'on peut le faire même avec un changement de variables, moi franchement je ne vois pas comment.

[Poulimi]

Bonjour, honnêtement je suis complètement perdu avec celle limite .

Avec la propriété de a^b
j'obtiens
exp((x+1/x²+1)ln((x^3+5)/(x²+2)))mais là du coup si j'ai bien compris je peux appliquer la fonctions logarithme à mon expression qui me donne donc
((x+1)/(x²+1))+ln(ln((x^3+5)/(x²+2))) je ne comprends pas

[Mikihisa]

Je ne sais pas, peut être en travaillant du des équivalence (mais attention ils fait faire attentions aux hypothèse nécessaire pour la composition a gauche par ln/exp) voir l'article wiki sur la composition des équivalence

[Poulimi]

Je ne sais pas, peut être en travaillant du des équivalence (mais attention ils fait faire attentions aux hypothèse nécessaire pour la composition a gauche par ln/exp) voir l'article wiki sur la composition des équivalence

Le problème , c'est que je suis en licence de chimie à part avoir fait de l'algèbre linéaire au semestre 1, je n'ai pas fait de maths... Et donc j'espérais pouvoir me débrouiller sans les équivalences car je ne maîtrise pas du tout en fait même si je sais qu'il faudra que j'y passe en attendant s'il faut utiliser les équivalences alors je pense que cette limite est d'un niveau trop difficile pour moi
en tout cas je te remercie pour tes suggestions :we:

[deltab]

Bonjour.

@ Poulimi
Ne perds pas espoir, tu peux la calculer avec les outils de terminale. Essaies de ramener pour le cas présent à la forme : , avec quand (Ici f(x), g(x) h(x) sont des fonctions rationnelles.
Je vais ti mettre un peu plus dans la voie: .
Le terme entre crochets tend vers, on peut l'écrire sous la forme avec
PS: Pour la F.I.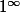 , on calcule aussi la limite du log sans oublier maintenant que

[Poulimi]

Bonjour.

@ Poulimi
Ne perds pas espoir, tu peux la calculer avec les outils de terminale. Essaies de ramener pour le cas présent à la forme : , avec quand (Ici f(x), g(x) h(x) sont des fonctions rationnelles.
Je vais ti mettre un peu plus dans la voie: .
Le terme entre crochets tend vers, on peut l'écrire sous la forme avec
PS: Pour la F.I. , on calcule aussi la limite du log sans oublier maintenant que

Bonsoir
Merci beaucoup pour l'aide mais déjà je ne suis pas sur si ma méthode est bonne pour me débarrasser de l'exponentiel quand j'ai a^b=exp(bln(a)) il faut donc que j'applique la fonction log qui va donc me permettre de faire ln(exp(bln(a))=bln(a) si j'ai bien compris ? puisque exp(ln(x))=x
Dans ce cas là je comprends le f(x)ln(g(x))

[Poulimi]

Bon je pense que c'est plus clair si je pars du principe que ce que j'ai noté avant est bon j'ai alors

(x+1)/(x²+2)ln((x^3+5)/(x²+2))=f(x)ln(g(x)) ?

Avec les éléments que tu m'as donné ça me donne
((x+1)/(x²+1))ln(x)+((x+1)/(x²+1))ln(1+(5/x^3)/(1+(2/x²)))

=((x+1)/(x²+2))ln(x)+((x+1)/(x²+1))fois((1+(5/x^3)/(1+(2/x²))-1)fois lni/J
en fait i c'est h(x)+1 et j c'est h(x) c'est vraiment très long à écrire

donc pour le deuxième terme mon taux d'accroissement tend vers 0 etdans le f(x)h(x)ln(1+h(x))/h(x) le h(x) avant le ln je le fais tendre POUR X vers +OO OUen 0 ?si je fais tendre ce h(x) en o j'ai une FI après si je fais tendre x vers +OO pour le f(x) ça tend vers 0 donc voilà et pour le premier terme est-il possible d'appliquer la règle de l'hôpital ?
Merci vraiment beaucoup

[deltab]

Il est quand même clair qu'on calcule les différentes limites pour 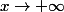(c'est la limite demandée), on n'a pas encore fait de changement de variables.
Il n'a pas de taux d'accroissement à l'infini. On s'y ramène par un changement de variables (Le principe de la règle de l'Hôpital est basée sur les taux d'accroissement)

[Poulimi]

Bonjour j'ai été absent pendant un moment afin d'être un peu plus clair sur les différentes façons d calculer les limites de fonctions et donc pour en revenir à la dernière je pense avoir trouvé grâce aux équivalents. Les outils de terminales me compliquent beaucoup trop les choses par moment
alors j'avais donc ((x^3+5)/(x²+1)^((x+1)/(x²+1)) après utilisation de a^b=exp(blna)
et après avoir utilisé la fonction ln pour simplifier j'obtiens donc ((x+1)/(x²+2))ln((x^3+5)/(x²+2))

en +OO l'équivalent d'un polynôme est son terme du plus haut degré par conséquent en +OO x+1 équivalent à x et x²+1 équivalent à x² par conséquent le quotient des ses deux polynômes en +oo est équivalent à 1/x concernant la fraction rationnelle prise dans le logarithme de même j'ai x^3+5 équivalent à x^3 et x²+1 et donc le quotient de mes deux polynômes en +OO est équivalent à x
en conclusion mon expression de départ est équivalent en +oo à ln(x)/x et cette limite en plus inf vaut 0

[Poulimi]

Est-ce bon de cette façon ? Merci

[deltab]

Bonjour

Est-ce bon de cette façon ? Merci

Le problème se situe au niveau du log, si on n'a pas .
C'est pour ça que j'ai introduit la fonction pour me ramener à ( quand )
PS:
On a bien quand , a-t-on

[Poulimi]

oh mince oui tu as raison je suis allé trop vite donc il n'y a aucun autre moyen à part utilisation de changement de variable et outils de terminales les dl par exemple en +OO je peux ?

Je vais continuer alors avec les indications que tu m'avais donné , encore merci!