Bonjour ! Est-ce que tu as vu les développements limités ? Si oui, utilise-les !
À la calculatrice je trouve que la limite vaut ~ 1,1158.
Il faut utiliser le fait que, pour a>0 et lorsque x tend vers 0 :
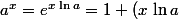 + \frac{1}{2!}(x\ln a)^2 + \cdots + \frac{1}{n!}(x\,\ln a)^n + x^n\epsilon(x).)
Ici tu l'appliques successivement aux quatre termes du numérateur, ou bien au produit
(2^x-1))
(plus simple). Je te laisse deviner à quel ordre on doit développer. Bien sûr il faut aussi développer le dénominateur.
À la fin j'ai trouvé [censuré], qui fait 1,115577... Ça colle !