Bonjour
Je voudrais savoir comment faire pour montrer que:
[aX^b+ (1-a)Y^b]^(1/b) = X^a . Y^(1-a)
Lorsque b=0
Merci beaucoup!
Petite démonstration
5 messages
- Page 1 sur 1
par Aktar » 07 Mar 2014, 16:29
paquito a écrit:Lorsque b=0, 1/b n'est pas défini! Regarde bien ton énoncé.
En faite c lorsque b tends vers 0. Faut faire une extension de Taylor
par paquito » 07 Mar 2014, 17:56
Aktar a écrit:En faite c lorsque b tends vers 0. Faut faire une extension de Taylor
Pose X^b=e^blnX et Y^b=e^blnY, b étant la variable. Après c'est du calcul pénible.
par Ben314 » 08 Mar 2014, 00:40
En supposant 
, 
(sinon ça a pas trop de sens) et en posant )
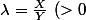on a :
Y^t\Big)^{\frac {1}{t}}=Y\Big(a\lambda^t+1-a\Big)^{\frac {1}{t}}=Y.\exp\Big(\frac{\ln(a\lambda^t+1-a)}{t}\Big))
Or, lorsque
, }{t}\)
tend vers )
où \)
(car =0)
).
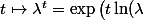Et, compte tenu du fait que la dérivée de\big)\)
est \lambda^t\)
on a =\frac{a\ln(\lambda)\lambda^t}{a\lambda^t+1-a}\)
d'où =a\ln(\lambda)\)
et l'expression de départ tend vers )=Y.\lambda^a=X^aY^{1-a})
Or, lorsque
Et, compte tenu du fait que la dérivée de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :