Algèbr - Matrices (niveau L2)

[ash09]

Bonjour à tous,
Je suis en train de plancher sur la question suivante :

Soit n>=2 un entier et E l'espace vectoriel contenant toutes les matrices réelles de taille nxn.

Soit D une matrice de E satisfaisant :
pour tout M appartenant à E, DM = MD.

Prouver qu'il existe un a réel tel que D = aI, I étant la matrice identité.

Je vous remercie de votre aide.

[Monsieur23]

Aloha,

Tu peux appliquer ton égalité DM=MD aux matrices Eij (matrice avec des 0 partout, sauf un 1 ligne i, colonne j).

[ash09]

Aloha,

Tu peux appliquer ton égalité DM=MD aux matrices Eij (matrice avec des 0 partout, sauf un 1 ligne i, colonne j).

Je ne comprends pas trop où tu veux en venir. Est-ce que tu pourrais donner plus de détails svp ?

[Monsieur23]

L'idée, c'est que les Eij forment une base de Mn(R) : tu peux écrire .

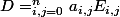
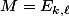
Ensuite, tu prends , et tu regardes ce que donne l'égalité DM=MD.

(Avant ça, tu peux calculer pour tous i,j,k,l)