Salut à tous.
J'aimerais savoir si on peut calcul la valeur myenne de l'accélération éxercée par laTerre sur un objet qui s'éloigne d'elle par:
;)_a^b(G M/R² dR)*(1/b-a), avec a l'altitude de départ, b celle d'arrivée, et R l'altitude à un moment donné.
Merci.
Raisonnement
12 messages
- Page 1 sur 1
par Doraki » 24 Déc 2010, 12:14
Là ce que tu décris c'est une moyenne spatiale, où tu intègres par rapport à l'espace.
Moi j'aurais plutôt imaginé que c'est la moyenne temporelle, où tu intègres par rapport au temps, qu'on demande.
Et les deux sont différents, c'est pour ça que demander une "moyenne" c'est souvent pas très clair.
Moi j'aurais plutôt imaginé que c'est la moyenne temporelle, où tu intègres par rapport au temps, qu'on demande.
Et les deux sont différents, c'est pour ça que demander une "moyenne" c'est souvent pas très clair.
par vincentroumezy » 24 Déc 2010, 12:58
Parcqu'en fait, je me demandais, pour une fusée, qui s'éloigne de la terre, à quelle accéleration elle est soumise en chaque ^oint.
Je ne saurais pas faire une moyenne temporelle, car la contrainte sur le trajet du véhicule est sur la distance parcourue.
Est-ce juste de l'utiliser dans des calcuks comme:
v=v0+at, ou a est l'accéleration moyenne, ou
h=v0t+(1/2)at² ?
Je ne saurais pas faire une moyenne temporelle, car la contrainte sur le trajet du véhicule est sur la distance parcourue.
Est-ce juste de l'utiliser dans des calcuks comme:
v=v0+at, ou a est l'accéleration moyenne, ou
h=v0t+(1/2)at² ?
par Doraki » 24 Déc 2010, 15:42
La seule relation valable, est que si a = la moyenne obtenue en faisant une intégrale sur le temps de t0 à t1, et si v0 = vitesse à t = t0, v1 = vitesse à t = t1, ben on a trivialement que v1 = v0 + a*(t1-t0).
Tout ce que tu peux imaginer d'autre sera bien sûr complètement faux.
Tout ce que tu peux imaginer d'autre sera bien sûr complètement faux.
par vincentroumezy » 26 Déc 2010, 19:08
Salut, l'autre égalité est elle juste pour une accélération moyenne par rapport au temps ?
par vincentroumezy » 28 Déc 2010, 13:31
Tu as raison, mais comment je déplace le post?
Et puis, il y'a peut etre plus de monde ici, qu'en section phyique.
Et puis, il y'a peut etre plus de monde ici, qu'en section phyique.
par Arnaud-29-31 » 28 Déc 2010, 17:06
Salut,
Oui on a bien une moyenne spatiale égale à
Si j'aborde le problème comme ceci :
Soit un point situé à une distance a du centre de la terre et un autre situé à une distance b.
Je réalise un découpage du segment reliant mes deux points avec un pas de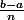
L'accélération subie due à l'attraction de la terre vaut au point premier point
, au deuxième ^2})
, au troisième ^2})
.... au (n+1)ième ^2} \left( = \frac{GM}{b^2} \right))
...
La moyenne de toutes ces accélérations vaut^2})
Et si je me trompe pas, tu veux la valeur de cette moyenne quand n tend vers l'infini ...
Somme de Riemann et on retrouve le résultat.
Oui on a bien une moyenne spatiale égale à
Si j'aborde le problème comme ceci :
Soit un point situé à une distance a du centre de la terre et un autre situé à une distance b.
Je réalise un découpage du segment reliant mes deux points avec un pas de
L'accélération subie due à l'attraction de la terre vaut au point premier point
La moyenne de toutes ces accélérations vaut
Et si je me trompe pas, tu veux la valeur de cette moyenne quand n tend vers l'infini ...
Somme de Riemann et on retrouve le résultat.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :