Probabilité de présence
De la mécanique au nucléaire, nos physiciens sont à l'écoute
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 28 Fév 2008, 20:32
par Babe » 28 Fév 2008, 20:32
Bonsoir,
j'ai un passage de mon cours que je peine un peu à comprendre
"on definit a chaque instant une probabilité dP de trouver la particule telle que
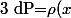d\tau)
avec
d\tau=1) Cela nous amène
Cela nous amène à classer les etats en 2: etats liés et etats non liés"
j'ai pas compris ce que signifie etats non liés et etats liés et pourquoi "cela nous amene"
merci d'avance
 par Dominique Lefebvre » 28 Fév 2008, 21:10
par Dominique Lefebvre » 28 Fév 2008, 21:10
Babe a écrit:Bonsoir,
j'ai un passage de mon cours que je peine un peu à comprendre
"on definit a chaque instant une probabilité dP de trouver la particule telle que

avec
 Cela nous amène
Cela nous amène à classer les etats en 2: etats liés et etats non liés"
j'ai pas compris ce que signifie etats non liés et etats liés et pourquoi "cela nous amene"
merci d'avance
Bonsoir,
Pour comprendre la notion d'état lié ou son contraire l'état non lié (ou de diffusion), il faut en revenir au mouvement d'une particule dans un potentiel V et à son énergie.
Si l'énergie E de la particule est >= V(infini) alors on a affaire à un état de diffusion (on dit aussi de collision ou non lié).
Si E < V(infini) on a affaire à un état lié.
Mathématiquement, une particule est dans un état énergétique lié lorsque sa fonction d'onde est solution de l'équation aux valeurs propres de l'hamiltonien H et qu'elle est de carré sommable. C'est de là que vient ton intégrale...
Physiquement, cela veut dire que notre particule est loclaisée dans un domaine fini de l'espace. Dans un état non lié, la particule ne reste pas localisée dans un domaine fini: c'est pour cela qu'on parle d'état de diffusion...
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 28 Fév 2008, 21:20
par Babe » 28 Fév 2008, 21:20
Dominique Lefebvre a écrit:Bonsoir,
Pour comprendre la notion d'état lié ou son contraire l'état non lié (ou de diffusion), il faut en revenir au mouvement d'une particule dans un potentiel V et à son énergie.
Si l'énergie E de la particule est >= V(infini) alors on a affaire à un état de diffusion (on dit aussi de collision ou non lié).
Si E < V(infini) on a affaire à un état lié.
Mathématiquement, une particule est dans un état énergétique lié lorsque sa fonction d'onde est solution de l'équation aux valeurs propres de l'hamiltonien H et qu'elle est de carré sommable. C'est de là que vient ton intégrale...
Physiquement, cela veut dire que notre particule est loclaisée dans un domaine fini de l'espace. Dans un état non lié, la particule ne reste pas localisée dans un domaine fini: c'est pour cela qu'on parle d'état de diffusion...
a ok merci dominique
je m'attendais à plus trivial que ca lol
(enfin le coté physique est toujours plus appreciable que le coté obscur de la force ...)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités

 avec
avec 