Geiger-Müller

[Jota Be]

Bonsoir,
J'ai été aujourd'hui amené à calculer une formule en exam, je me demande si elle est juste.
On considère une sphère de rayon d contenant un échantillon radioactif de . Un compteur de Geiger-Müller est localement placé dans la paroi, et nous nommons S la surface du compteur qui dénombre les particules. L'échantillon se trouve au centre donc à une distance d du compteur.
Nous savons aussi que avec C(t) le nombre de particules comptées en fonction du temps et A l'activité physique de l'échantillon.
J'ai trouvé que
avec l'aire de l'ouverture du compteur, la durée d'un comptage et l'efficacité du detecteur (proportion de particules entrant dans le compteur qui sont détectées).
Cette formule est de même homogène à un temps, ce qui est conforme avec les données de l'énoncé, mais je ne sais vraiment pas si elle est juste et comment la démontrer, parce que j'y suis un peu allé à tâtons...
Merci de m'indiquer la voie (rien de pressant, c'est passé désormais)

[Mathusalem]

Bonsoir,
J'ai été aujourd'hui amené à calculer une formule en exam, je me demande si elle est juste.
On considère une sphère de rayon d contenant un échantillon radioactif de . Un compteur de Geiger-Müller est localement placé dans la paroi, et nous nommons S la surface du compteur qui dénombre les particules. L'échantillon se trouve au centre donc à une distance d du compteur.
Nous savons aussi que avec C(t) le nombre de particules comptées en fonction du temps et A l'activité physique de l'échantillon.
J'ai trouvé que
avec l'aire de l'ouverture du compteur, la durée d'un comptage et l'efficacité du detecteur (proportion de particules entrant dans le compteur qui sont détectées).
Cette formule est de même homogène à un temps, ce qui est conforme avec les données de l'énoncé, mais je ne sais vraiment pas si elle est juste et comment la démontrer, parce que j'y suis un peu allé à tâtons...
Merci de m'indiquer la voie (rien de pressant, c'est passé désormais)

Salut.
La clé c'est de dire que quand l'échantillon se décompose, le rayon qu'il emet va équiprobablement dans n'importe quelle direction (donc si tu veux t'as une probabilité uniforme de toucher n'importe quel point d'une sphère centrée sur l'échantillon). Ainsi, la probabilité que le rayon passe dans une surface S de la sphère, c'est simplement (loi uniforme).

Maintenant, ça, ça reste une probabilité. Mais puisque le temps de mesure est pas trop petit, et la quantité d'émissions de l'échantillon est (en général) colossal, sur N émissions, tu peux affirmer que tu en détecteras N*P (ce qui n'est pas le cas si ton temps de mesure est très court par rapport au nombre d'émissions. Si l'échantillon ne fait que 10 émissions, bha c'est pas vraiment assez, et tu vas surement pas en détecter 10*P)

Donc effectivement, puisque A(t) est un nombre d'emission par secondes qui varie lentement avec le temps, tu peux facilemnt affirmer que = le nombre d'émissions dans un laps de temps .

Ainsi,


Tu peux également supposer que l'efficacité du détecteur est caractérisée par un nombre E entre 0 et 1, alors



Et tu as bien

[Jota Be]

Bonsoir Mathusalem et merci pour ta réponse !

Salut.
La clé c'est de dire que quand l'échantillon se décompose, le rayon qu'il emet va équiprobablement dans n'importe quelle direction (donc si tu veux t'as une probabilité uniforme de toucher n'importe quel point d'une sphère centrée sur l'échantillon). Ainsi, la probabilité que le rayon passe dans une surface S de la sphère, c'est simplement (loi uniforme).

Ok, j'ai compris, mais je ne savais pas que ça s'appelle loi uniforme !

Maintenant, ça, ça reste une probabilité. Mais puisque le temps de mesure est pas trop petit, et la quantité d'émissions de l'échantillon est (en général) colossal, sur N émissions, tu peux affirmer que tu en détecteras N*P (ce qui n'est pas le cas si ton temps de mesure est très court par rapport au nombre d'émissions. Si l'échantillon ne fait que 10 émissions, bha c'est pas vraiment assez, et tu vas surement pas en détecter 10*P)

Si je te suis, cela signifie que les émissions N sont discrètes, non ? Ok
Mais je croyais qu'une émission se faisait aléatoirement dans le temps et qu'une particule éjectée était UNE seule émission...
Je croyais aussi que le nombre de particules par émissions décroissait en fonction du temps. Ce P est-il donc la valeur moyenne de particules observées sur N émissions en fonction de Dt ?
Je pense ne pas avoir très bien compris cette partie.

[Mathusalem]

Bonsoir Mathusalem et merci pour ta réponse !

Ok, j'ai compris, mais je ne savais pas que ça s'appelle loi uniforme !

Si je te suis, cela signifie que les émissions N sont discrètes, non ? Ok
Mais je croyais qu'une émission se faisait aléatoirement dans le temps et qu'une particule éjectée était UNE seule émission...
Je croyais aussi que le nombre de particules par émissions décroissait en fonction du temps. Ce P est-il donc la valeur moyenne de particules observées sur N émissions en fonction de Dt ?
Je pense ne pas avoir très bien compris cette partie.

Je sais pas si j'ai bien compris ce que tu n'as pas compris

Il y a plein de sorte de desintegration differentes. Pour simplifier, prenons la desintegration beta-.

1. Tu as un noyau atomique lourd, par exemple l'Americium . Pour certaines raisons, il s'avere qu'au cours du temps, un neutron du noyau se convertira en proton. La configuration electronique de ce nouveau noyau est instable (pas favorable energetiquement). Alors, le proton va descendre dans un niveau d'energie plus bas, emettant ainsi un rayonnement (rayon gamma je crois dans ce cas). C'est ce rayonnement que tu vas mesurer (en gros tu vas detecter un photon hautement energetique).

2. Tu ne peux pas predire quand cette desintegration aura lieu, mais la probabilite de desintegration est la meme pour n'importe quel temps.

3. Tu consideres maintenant un echantillon d'Americium, dans lequel se trouvent typiquement (Nombre d'Avogadro) atomes d'Americium, donc autant d'emetteurs. Chaque noyau a la meme probabilite de se desintegrer, donc pendant un intervalle de temps dt, le nombre de de desintegrations (donc d'emissions) -dQ que tu vas mesurer est propotionnel au nombre d'emetteurs Q de ton echantillon.

Note que y a un signe moins devant dQ, parce que une desintegration signifie une diminution du nombre Q d'emetteurs.
Donc tu trouves .
Le nombre d'emetteurs que tu as diminue exponentiellemnt avec le temps. On appelle la constante de desintegration. Plus elle est grande, moins le noyau se desintegre vite. C'est donc en rapport direct avec la probabilite de desintegration du noyau.
Bref, ton activite est donc puisque la difference entre le nombre de noyaux initiaux et le nombre de noyaux aux temps t est precisement le nombre d'emissions qui ont eu lieu. Tu vois donc que le nombre d'emissions en fonction du temps est enfait immense.

4. Typiquement, le temps de demi-vie () varie de 1 a 1000 ans, grossierement.
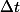
Donc, pendant une mesure , le nombre d'emissions faite sera a une tres bonne approximation , si bien entendu le temps de mesure est petit devant le temps de demi-vie. Autrement, l'activite varie trop fortement pendant la mesure pour voir la considerer constante - ce qui repond a ta question quant a la decroissance de l'activite.
-----
Donc jusque la, c'est pour justifier que pendant un intervalle de temps assez court, un echantillon fait d'environ 10^23 emetteurs emets une quantite phenomenale (typiquement 10^12 emissions/seconde) de rayons, et cette quantite est a une bonne approximation constante.

L'autre argument pour ton probleme, c'est de dire que chaque rayon est emis dans une direction aleatoire. Puisque t'es dans l'espace 3D, ca veut dire que si tu centres une sphere sur l'echantillon, le photon emis passera avec la meme probabilite par chaque point de la sphere.
Si t'appeles A la surface de la sphere, et S ta fenetre dans la sphere, alors la probabilite que ton rayon emis passe par S est de S/A.

Maintenant, imagine que tu emettes seulement 15 rayonnement par seconde. Alors ca n'a pas de sens de dire que tu vas detecter S/A*15 rayonnement dans le detecteur. Le nombre de rayonnements n'est pas suffisamment grand. Par contre, avec 10^12 rayonnements par seconde, la, c'est deja assez certain de dire que tu vas avoir en moyenne S/A*10^12 rayonnements qui passent dans ta fenetre en une seconde (ce serait denouveau absurde d'affirmer cela, si par exemple ton temps de mesure etait de 10^{-12} secondes)

D'ou le calcul fait.

C'est long mais j'espere que c'etait clair.

[Jota Be]

Tout d'abord, merci pour le message, il y a de quoi lire en effet (y)
Je vais essayer de digérer ça dans la soirée et je te dirai s'il y a quelque chose que je ne comprends pas !
Merci encore, Mathusalem

PS : est-ce que tu pourrais me repasser le lien de ton site pour le logiciel Latex, s'il-te-plait ?

[Mathusalem]

Tout d'abord, merci pour le message, il y a de quoi lire en effet (y)
Je vais essayer de digérer ça dans la soirée et je te dirai s'il y a quelque chose que je ne comprends pas !
Merci encore, Mathusalem

PS : est-ce que tu pourrais me repasser le lien de ton site pour le logiciel Latex, s'il-te-plait ?

C'etait pas moi pour le logiciel Latex... Je crois qu'Olympus avait poste un truc bien, mais sans conviction.

[Jota Be]

C'etait pas moi pour le logiciel Latex... Je crois qu'Olympus avait poste un truc bien, mais sans conviction.

si pourtant, il me semble bien que c'était toi, tu me l'avais passé un jour. Je ne vois pas qui d'autre ça pourrait être.

EDIT : si, maintenant je vois qui c'est. Mathémartiste. Mathusalem, Mathémartiste, il y a de quoi confondre :zen: