Electrostatique !

[barbu23]

Bonjor à tous : :happy3:
Je voudrais savoir ce q'on entend en éléctrostatique, par "plan" de sysmetrie d'un problème !Vous pouvez me donner un petit exemple qui illustre ce fait là avec des calculs si possibles du champ et de force éléctrostatique ?
Merci infiniment ! :happy3:

[switch_df]

N ayant jamais vu ce terme défini je suppose simplement que ton problème particulier possède un plan de symétrie et que ça doit forcément t'aider à résoudre ce que tu cherches. Est-ce possible?

[Benjamin]

Bonsoir,

Un plan de symétrie tout court, ça ne renseigne pas beaucoup. Par contre, dire qu'un plan est un plan de symétrie pour la distribution des charges par exemple, ça aide pas mal. En effet, le principe de Pierre Curie dit que "un phénomène physique possède au moins les mêmes symétries que les causes qui le produisent." Ainsi donc, une symétrie sur la distribution de charges, sources du champ E et du potentiel V, se répercutent intégralement sur E et V.

[Benjamin]

Exemple :
Calcul du champ (le début) créé par un disque uniformément chargé en un point M de son axe (on va dire l'axe z'z, avec le disque placé en z=0).

Déjà, le plan du disque est un plan de symétrie (un plan d'invariance) pour la distribution de charges, donc si M' est l'image de M par ce plan, V(M')=V(M) (V(-z)=V(z), le plan de symétrie donne une fonction paire) et E(M') est le symétrique de E(M) par ce plan.

Ensuite, les plans perpendiculaires au disque et contenant l'axe sont des plans de symétries pour la distribution. Or le champ créé par une distribution en un point d'un plan de symétrie de cette distribution appartient à ce plan (je te laisse voir pourquoi), donc dans notre cas, E(M) appartient à l'ensemble de ces plans, donc à leur intersection, donc le champ est dirigé par l'axe. Ainsi, E(M)=E(M)u_z. Bien pratique à savoir pour utiliser le théorème de Gauss par la suite pour finir cet exercice

[barbu23]

Merci bcp "bengamin" et "switch" pour ces precisions ! :happy3:
Justement, j'ai aussi quelques souci concerant le théorème de Gauss ! J'ai l'énoncé suivant qui dit que :
Le flux de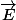 généré par une distribution de charges éléctrostatiques ( charge totale ) sortant d'une surface fermée est nulle si la charge est à l'exterieur de la surface ( surface de Gauss ) et vaut : si la charge est à l'interieur de :
On a :

ça fait des années que j'ai pas jeté un oeil sur ce cours, et si mes souvenirs sont bons, Une surface de Gauss est par exemple une sphère d'un balon n'est ce pas ? elle est fermée et donc s'il n'y'a pas de charges à l'interieur du balon alors le flux vers l'exterieur de la surface vaut . par contre, s'il y'a des charges à l'interieur du balon, alors le flux vers l'exterieur vaut :
N'est ce pas ? :happy3:
Merci d'avance ! :happy3:

[Benjamin]

Pour moi, c'est très mal dit. Je ne dis pas le flux sortant d'une surface fermée, mais le flux à travers. Alors je pense qu'ils disent sortant pour préciser l'orientation de la surface fermée, mais comme par convention, une surface fermée voit ses vecteur dS orientés vers l'extérieur, ça pose pas trop de problème.
Bref, une surface de Gauss est ce que tu veux. Tu peux prendre le truc le plus alambiqué qui soit. Même une surface fractale si ça t'amuse. Le théorème est valable quelle que soit la surface. C'est juste que selon les cas, les calculs sont simples ou compliqués ;). Si tu as un problème à symétrie sphérique, en général, tu prendras comme surface du Gauss une sphère oui. Et les charges intérieures ou extérieures sont effet positionnées comme telle par rapport à la surface de Gauss.
En te lisant, il me semble que tu as bien compris en tout cas.