Cyclotron
De la mécanique au nucléaire, nos physiciens sont à l'écoute
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
par sue » 08 Avr 2007, 13:56
Bonjour,
on injecte un faisceau de proton au centre
d'un Cyclotron sans vitesse initiale .
la 1ère question est de déterminer le nombre des tours réalisé par un proton avant qu'il quitte le Cyclotron .
2) montrer que la distance parcourue par le proton vérifie la relation :
)
t.q n est le nombre des demi-tours parcourus .
données : R=1m U=1 kV B=0,2T
R : rayon du dernier demi-tour .
---
voilà je bloque sur ces deux questions , j'ai besoin juste de qqs indications .
merci
par Dominique Lefebvre » 08 Avr 2007, 14:22
sue a écrit:Bonjour,
on injecte un faisceau de proton au centre [url="http://www.sciences.univ-nantes.fr/physique/perso/gtulloue/Meca/Charges/cyclotron.html"]d'un Cyclotron[/url]sans vitesse initiale .
la 1ère question est de déterminer le nombre des tours réalisé par un proton avant qu'il quitte le Cyclotron .
2) montrer que la distance parcourue par le proton vérifie la relation :
t.q n est le nombre des demi-tours parcourus .
données : R=1m U=1 kV B=0,2T
R : rayon du dernier demi-tour .
---
voilà je bloque sur ces deux questions , j'ai besoin juste de qqs indications .
merci
Bonjour Sue (re..)
Première indication, que tu connais certainement: lesprotons parcourent des trajectoires en demi-cercle dans les "D". Le rayon de la trajectoire dépend de la vitesse v selon l'équation r = mv/qB.
A chaque passage dans les "D", le proton acquière de l'énergie dE = qU. Sur le demi-cercle numéro n, on peut écrire (1/2)mvn^2 = nqU et son rayon est rn = mvn/qB.
Tu peux en déduire le rapport des rayons des demi-cercles consécutifs!
Rn+1/R = sqrt((n+1)/n)
A toi de jouer...
Nota : je note la charge du proton q et toi tu la notes e...
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
par sue » 08 Avr 2007, 14:49
ah bah merci bien , je crois que j'ai pigé ce qu'il faut faire pour la 2ème question .
on a :
.
.
on a aussi :
donc en sommant les égalité on obtient :
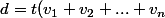 = \frac{\pi m}{eB} (\sqrt{\frac{2eU}{m}} + \sqrt{2}\sqrt{\frac{2eU}{m}}+...+\sqrt{n} \sqrt{\frac{2eU}{m}})= \frac{\pi m}{eB}\sqrt{\frac{2eU}{m}}(1+\sqrt{2}+....+\sqrt{n})<br />=\frac{\pi}{B}\sqrt{\frac{2mU}{e}}(1+\sqrt{2}+....+\sqrt{n}))
sinon je réfléchis encore à la première question suivant tes indications ... :we:
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
par sue » 08 Avr 2007, 16:03
c'est bizarre , je ne trouve toujours pas le nombre de tours ...
j'essaye d'exploiter la dernière donnée concernant le rapport de 2 rayons consécutifs , mais je vois pas encore le rapport ...
j'essaye autre chose ..
on utilisant la relation indépendante du temps on :
)
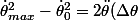soit :
)
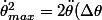(vitesse initiale nulle)
aprés j'utilise
avec n le nombre des tours .
on peut trouver
puisqu'on a
et on a l'accélération angulaire constante donc on peut en déduire n .
est-ce juste ? :hein:
par Dominique Lefebvre » 08 Avr 2007, 17:23
sue a écrit:c'est bizarre , je ne trouve toujours pas le nombre de tours ...
j'essaye d'exploiter la dernière donnée concernant le rapport de 2 rayons consécutifs , mais je vois pas encore le rapport ...
j'essaye autre chose ..
on utilisant la relation indépendante du temps on :
soit :
(vitesse initiale nulle)
aprés j'utilise
avec n le nombre des tours .
on peut trouver
puisqu'on a
et on a l'accélération angulaire constante donc on peut en déduire n .
est-ce juste ? :hein:
Je crois qu'on peut raisonner plus simplement:le proton quitte le cyclotron lorsque la rayon de sa dernière trajectoire est égal au rayon R du cyclotron.
Comme on sait que Rn = sqrt(2mU/qB^2)*sqrt(n). et que lorsque le proton sort pour N = n/2,N le nombre de tours pour sortir, alors: N = qR^2B^2/4mU
Je trouve environ 1000 tours, et toi?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
par sue » 08 Avr 2007, 19:28
ah ben c bien ça ce que je cherchais , sans doute plus simple , merci :we:
mais bon moi je trouve environ 958 tours :hein:
en tout cas merci bien Dominique !
ps: tu peux me répondre sur l'autre sujet 'oscillateurs' si ça ne vous dérange pas !
par Dominique Lefebvre » 08 Avr 2007, 22:02
sue a écrit:ah ben c bien ça ce que je cherchais , sans doute plus simple , merci :we:
mais bon moi je trouve environ 958 tours :hein:
en tout cas merci bien Dominique !
ps: tu peux me répondre sur l'autre sujet 'oscillateurs' si ça ne vous dérange pas !
En fonction de mes approx, je suis exactement à 963 tours! On ne va pas chipoter...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
