@upium666
Quand tu écris
)
, cela veut dire que :
)
sont les coordonnées dites cartésiennes du vecteur

dans une base
)
donnée du plan (vectoriel)
Et on a :
 Remarques
Remarques :
1) le plan vectoriel est muni d'un "opérateur entre les vecteurs" qui s'appelle
le produit scalaire (que tu vas étudier cette année)
2) la base
)
est généralement orthonormée
Maintenant si
 (car la notion d'angle nécessite que les vecteurs ne soient pas nuls),
(car la notion d'angle nécessite que les vecteurs ne soient pas nuls), on peut définir le vecteur

par
2 autres nombres )
qui sont
les coordonnées dites trigonométriques de ce vecteur
et qui sont définies par
1) 
(la norme du vecteur)
2) l'angle
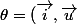)
Pour mesurer cet angle
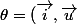)
on peut
soit utiliser un rapporteur
soit utiliser les fonctions trigonométriques
cosinus et
sinus car on a :
=\frac{x}{\sqrt{x^2+y^2}})
et
=\frac{y}{\sqrt{x^2+y^2}}) Conclusion
Conclusion Soit
)
et
)
2 vecteurs non nuls
l'angle
 = (\vec{u},\vec{i}) + (\vec{i},\vec{v}) = (\vec{i},\vec{v}) - (\vec{i},\vec{u}))
(relation de Chasles)
ET donc l'angle
=\theta ' -\theta)
ET on appelle
mesure principale d'un angle la mesure de cet angle en radians qui appartient à

J'espère que tu as compris ces explications
A+
ps)Quand tu auras étudié le produit scalaire , tu auras une formule du type
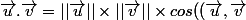)=xx' + yy')
qui permet d'obtenir une mesure de l'angle
(non orienté) entre ces 2 vecteurs