Bonjour à toutes et à tous,
J’ai un devoir maison pour demain sur lequel j’ai quelques difficultés.
Voici l’énoncé :
J’ai : A = 1 + ( 1/1+1) B=1+ (1/1+A) C= 1+ (1/1+B) et D= 1 + (1/1+C)
1/ exprimer c et d en fonction de A
Pour moi il s’agit de mettre a dans c donc :
Donc réécrire c en remplaçant le b par sa forme :1+ (1/1+A)
Mais le résultat me paraît trop complexe à utiliser
Je loupe l’essentiel il me semble .
Valeur approchée de la racine de deux
3 messages
- Page 1 sur 1
Re: Valeur approchée de la racine de deux
Bonjour,
A = 1 + ( 1/1+1) B=1+ (1/1+A) C= 1+ (1/1+B) et D= 1 + (1/1+C)
C=1+(1/(1+1+(1/(1+A))))
En remplaçant C par ce résultat on obtient:
D=...
A = 1 + ( 1/1+1) B=1+ (1/1+A) C= 1+ (1/1+B) et D= 1 + (1/1+C)
C=1+(1/(1+1+(1/(1+A))))
En remplaçant C par ce résultat on obtient:
D=...
Re: Valeur approchée de la racine de deux
Bonjour
Si on ne connait pas l'écriture Latex il faut au moins connaître l'usage des parenthèses
ici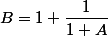
La première opération à effectuer est 1+A, il faudra donc la mettre entre parenthèses ensuite la division ayant priorité sur l'addition donc il n'est pas nécessaire d'utiliser d'autres parenthèses.
Avec des parenthèses cela donne B=1+1/(1+A)
elies934403 a écrit:Voici l’énoncé :
J’ai : A = 1 + ( 1/1+1) B=1+ (1/1+A) C= 1+ (1/1+B) et D= 1 + (1/1+C)
Si on ne connait pas l'écriture Latex il faut au moins connaître l'usage des parenthèses
ici
La première opération à effectuer est 1+A, il faudra donc la mettre entre parenthèses ensuite la division ayant priorité sur l'addition donc il n'est pas nécessaire d'utiliser d'autres parenthèses.
Avec des parenthèses cela donne B=1+1/(1+A)
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
