Trouver le centre d'un arc de cercle grace a deux point et u

[FlaMMe34]

Bonjour,
ca fait un bon moment que j'ai quitté les banc de l'école mais la je suis obligé de mi replongé pour le boulot.

Voila je cherche a trouver le centre de courbure d'un arc de cercle, sachant que je connais les coordonnée des extrémités de cet arc, l'angle de parcours de cet arc et le rayon de courbure de cet arc.

[chan79]

Bonjour,
ca fait un bon moment que j'ai quitté les banc de l'école mais la je suis obligé de mi replongé pour le boulot.

Voila je cherche a trouver le centre de courbure d'un arc de cercle, sachant que je connais les coordonnée des extrémités de cet arc, l'angle de parcours de cet arc et le rayon de courbure de cet arc.

Salut
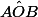
On connait les coordonnées de A et B et l'angle et on cherche les coordonnées de O. C'est bien ça ?

[FlaMMe34]

Salut
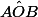
On connait les coordonnées de A et B et l'angle et on cherche les coordonnées de O. C'est bien ça ?

oui on connait également le rayon = OA = OB

[WillyCagnes]

bonjour,
l'équation du cercle : X² +y² =R²

le pt A appartient au cercle d'où Xa²+Ya²=R² (Xa et Ya les coordonnées du Pt A)
idem pour le pt B : Xb² +Yb² =R²

le centre O de coordonnées X0 et Y0

on calcule le rayon AO on a AO² =(Xa-X0)² +(Ya-Y0)² =R²
idem pour le rayon BO on a BO² =(Xb-X0)² +(Yb-Y0)² =R²

tu developpes puis simplifies, tu as 2 equations pour trouver Y0 et X0 donc pas besoin de connaitre l'angle de l'arc.

[chan79]

oui on connait également le rayon = OA = OB

O est sur la médiatrice de [AB]
Tu peux obtenir l'équation de cette médiatrice.
O est aussi sur le cercle de centre A et de rayon r connu.
Tu peux obtenir une équation de ce cercle.
Attention car une relation doit être respectée:

AB=2r*sin(a/2) avec a=

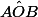
[Dlzlogic]

Bonjour,
Sans être plus curieux que nécessaire, je pense qu'il faudrait savoir quel est l'origine de cette question : besoin de formation continue ou problème réel.
Dans la pratique (en tout cas dans ma spécialité) on n'utilise rarement la méthode qui consiste à écrire l'équation d'une droite ou d'un cercle. On résout un ou des triangles et on calcule les coordonnées des points cherchés par la méthode des coordonnées polaires.
J'ajouterai qu'il y a deux solutions possibles (à droite ou à gauche de AB) et des données en surnombre.
Concernant les données en surnombre, soit on calcule cela selon les règles de l'art (difficile) soit on choisi de ne pas tenir compte d'une donnée, on calcule le résultat et enfin on vérifie que c'est correct.

[chan79]

Bonjour,
Sans être plus curieux que nécessaire, je pense qu'il faudrait savoir quel est l'origine de cette question : besoin de formation continue ou problème réel.
Dans la pratique (en tout cas dans ma spécialité) on n'utilise rarement la méthode qui consiste à écrire l'équation d'une droite ou d'un cercle. On résout un ou des triangles et on calcule les coordonnées des points cherchés par la méthode des coordonnées polaires.
J'ajouterai qu'il y a deux solutions possibles (à droite ou à gauche de AB) et des données en surnombre.
Concernant les données en surnombre, soit on calcule cela selon les règles de l'art (difficile) soit on choisi de ne pas tenir compte d'une donnée, on calcule le résultat et enfin on vérifie que c'est correct.

Bonjour Dlzlogic
Je suis d'accord, cet exo mériterait un peu plus d'explications.

[FlaMMe34]

Cette problématique est un problème réel. Il s'agit d'un calcul à intégrer dans un logiciel de CAO.

Je cherche à créer des arcs dont je peut faire bouger les extrémités et dont certaines propriété se mettent à jour toute seules et notamment les coordonnées du centre de courbure de l'arc.

si il est possible d'obtenir une solution plus simple à mettre en place je suis preneuse.

[Dlzlogic]

Bon, puisqu'il s'agit de CAO, il s'agit de conception.
Il y a pas mal de méthodes pour déterminer un arc de cercle, en vrac :
1- l'arc est défini par 3 points appartenant à l'arc
2- l'arc est défini par son centre, son rayon, l'angle de départ et l'angle d'arrivée
3- l'arc est défini par son point de départ, son centre et son point d'arrivée
4... etc.

J'ai établi un traitement de toutes les possibilités et tous les cas de calcul d'un arc de cercle, suivant leur définition (point de passage-droite ou cercle tangent, rayon etc.).

Tout problème comporte une solution, mais pour l'instant, on ne connait pas vraiment le problème.
En général, il est assez difficile de connaitre un angle au centre, cette valeur est très utilisée en calcul, mais pas vraiment en donnée de base. Il faudrait donc des détails.

[FlaMMe34]

Dans mon cas il s'agit de :
- l'arc est défini par son centre, son rayon, l'angle de départ et l'angle d'arrivée

Cependant je souhaite pouvoir modifier la position de l'une de mes extrémités et que ces propriétés se recalcule en fonction de cette nouvel position, sachant que je souhaite que le rayon de mon arc ne soit pas modifié.

[Dlzlogic]

Ce serait pas la méthode Autocad, par exemple ?
Soit xO et yO les coordonnées du centre et R le raton.
Je suppose que les angles sont des directions par rapport à une référence fixe, l'axe de Y par exemple,et un sens conventionnel, par exemple le sens des aiguilles d'une montre.
Alors les extrémités A et B sont définies par
xA = xO + R * sin(gA);
yA = yO + R * cos(gA);

xB = xO + R * sin(gB);
yB = yO + R * cos(gB);

gA et gB sont les angles de O vers A et de O vers B

Maintenant, supposons que vous ayez modifié le point A, vous connaissez les nouvelles valeurs xA et yA, il faut calculer le point O.
j'appelle gAB l'angle de A vers B et dAB la distance AB.
gAB = atan((yB-yA)/(xA-xB)).
Je vous conseille vivement d'utiliser la fonction atan2(Y,X)
dAB = sqrt((xB-xA)*(xB-xA)+(yB-yA)*(yB-yA))
Ang= gAB + acos((dAB/2) / R) ou Ang= gAB - acos((dAB/2) / R) suivant le sens : O à droite ou à gauche de AB.
xO = xA + R * sin(Ang)
yO = yA + R * cos(Ang)

Je crois que j'ai tout dit.

[FlaMMe34]

Ce serait pas la méthode Autocad, par exemple ?
Soit xO et yO les coordonnées du centre et R le raton.
Je suppose que les angles sont des directions par rapport à une référence fixe, l'axe de Y par exemple,et un sens conventionnel, par exemple le sens des aiguilles d'une montre.
Alors les extrémités A et B sont définies par
xA = xO + R * sin(gA);
yA = yO + R * cos(gA);

xB = xO + R * sin(gB);
yB = yO + R * cos(gB);

gA et gB sont les angles de O vers A et de O vers B

Maintenant, supposons que vous ayez modifié le point A, vous connaissez les nouvelles valeurs xA et yA, il faut calculer le point O.
j'appelle gAB l'angle de A vers B et dAB la distance AB.
gAB = atan((yB-yA)/(xA-xB)).
Je vous conseille vivement d'utiliser la fonction atan2(Y,X)
dAB = sqrt((xB-xA)*(xB-xA)+(yB-yA)*(yB-yA))
Ang= gAB + acos((dAB/2) / R) ou Ang= gAB - acos((dAB/2) / R) suivant le sens : O à droite ou à gauche de AB.
xO = xA + R * sin(Ang)
yO = yA + R * cos(Ang)

Je crois que j'ai tout dit.

Les angles angle du Début et angle de l'arc sont des angles par rapport au centre de l'arc de cercle, comme sur un cercle trigonométrique.

[Dlzlogic]

Les angles de début et de fin sont les directions des vecteurs OA et OB.
Un angle est souvent compris comme "le nombre de degrés de l'angle intérieur d'un triangle". Ici, il s'agit de l'indication angulaire de la direction. Moi j'appelle ça "gisement".
Cela ne veut pas dire grand-chose "angle par rapport à un point". Un angle, c'est par rapport à une direction. S'il y a "angle de départ" et "angle d'arrivée" ce sont des angles par rapport à une direction donnée. La direction choisie est généralement en option (choix de l'utilisateur), cela peut être l'axe des X vers l'est, ou l'axe des Y vers le nord, rarement autre chose.
Idem pour le sens, ça peut être le sens des aiguilles d'une montre, ou le sens trigo, là y'a pas d'autres possibilités.

[FlaMMe34]

Les angles de début et de fin sont les directions des vecteurs OA et OB.
Un angle est souvent compris comme "le nombre de degrés de l'angle intérieur d'un triangle". Ici, il s'agit de l'indication angulaire de la direction. Moi j'appelle ça "gisement".
Cela ne veut pas dire grand-chose "angle par rapport à un point". Un angle, c'est par rapport à une direction. S'il y a "angle de départ" et "angle d'arrivée" ce sont des angles par rapport à une direction donnée. La direction choisie est généralement en option (choix de l'utilisateur), cela peut être l'axe des X vers l'est, ou l'axe des Y vers le nord, rarement autre chose.
Idem pour le sens, ça peut être le sens des aiguilles d'une montre, ou le sens trigo, là y'a pas d'autres possibilités.

ici la direction serait la demi-ligne horizontal,partant du point O, et allant vers l'est.

en gros comme ci O était le centre du repère. or il ne l'est pas.

[CENTER][/CENTER]

[Dlzlogic]

Dans votre cas de figure, l'origine des angles est l'axe des X dans sens de X positifs, la direction OA, environ 40° et l'angle OB environ 100°.
L'angle au centre en O est 100° - 40° = 60°.
la position de O par rapport au repère n'a pas de relation avec le calcul des angles.
Si vous déplacez la figure de façon à avoir (0;0) pour coordonnées du point O, ça ne change rien concernant les angles.
Vous ne m'avez pas dit avec quel logiciel vous travaillez, c'est Autocad ou pas ?
Etes-vous sûres que la convention des angles est celle-là ?
Si vous me donnez un exemple numérique, coordonnées du point O, l'angle de départ, l'angle d'arrivée et le rayon, puis la nouvelle position du point A, je peux vous faire le calcul, vous pourrez ainsi vérifier.

[chan79]

Ce qui suit n'est pas niveau lycée, je pense. C'est juste pour voir si ça correspond au problème posé.
A priori, si on donne l'angle a (orienté) et les coordonnées de A et B, je partirais de l'égalité matricielle liée à la rotation d'angle a et de centre O.



Cela amène à un système de deux équations à deux inconnues (x(O) et y(O))
Ainsi pour A(5;2) et B(2;1) et pour un angle de , on obtient

O(4,3660254;-1,09807621)

C'est facile ensuite d'obtenir la distance OA.



Uploaded with ImageShack.us

[Dlzlogic]

Bonjour,
Je crois que la difficulté de compréhension vient de la définition du terme "angle".
Dans le manuel DXF les codes de groupe 50 et 51 donnent "angle de départ" et "angle final".
Ce terme "angle" signifie "angle de la direction concernée par rapport à la direction de base".
Comme je l'ai dit dans un message précédent, le choix de la direction de base dépend de l'utilisateur.
Dans ton exemple, Chan, l'angle de départ serait environ 75° et l'angle final 135°, soit l'angle [AOB] = 60°. (selon les conventions supposées).
Cela n'a pas de relation avec la position de la figure par rapport à l'origine.
Bien sûr, tout ceci dans le contexte de l'utilisation des logiciels de CAO/DAO en particulier.
Cette utilisation des coordonnées polaires est celle que l'on emploie en topographie, en navigation et je ne sais quoi. Peut-être que le remplacement du terme "angle" par "azimut" éclairerait la discussion.

[FlaMMe34]

Vous ne m'avez pas dit avec quel logiciel vous travaillez, c'est Autocad ou pas ?

Non ce n'est pas Autocad mais un logiciel que je suis entrain de développer.
et c'est dans le but de développer ce logiciel que je posais la question.

J'ai réussi a me débrouillé avec le système d’équation

(Xa-X0)² +(Ya-Y0)² =R²
(Xb-X0)² +(Yb-Y0)² =R²

Merci quand même de votre aide

[chan79]

Non ce n'est pas Autocad mais un logiciel que je suis entrain de développer.
et c'est dans le but de développer ce logiciel que je posais la question.

J'ai réussi a me débrouillé avec le système d’équation

(Xa-X0)² +(Ya-Y0)² =R²
(Xb-X0)² +(Yb-Y0)² =R²

Merci quand même de votre aide

Pourquoi nous parler d'angles ????