Trigonométrie

par **PRC** » 02 Nov 2012, 19:01

Bonsoir,

Je n'arrive pas à justifier la dérivabilité de

sur [0;

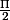
[ :mur: ...

Quelqu'un pourrait-il me donner une piste :id: ... ?

Merci :we: !

par **Vat02** » 02 Nov 2012, 21:51

PRC a écrit:Bonsoir,

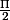
Je n'arrive pas à justifier la dérivabilité de sur [0;[ :mur: ...

Quelqu'un pourrait-il me donner une piste :id: ... ?

Merci :we: !

tan(t) = sin(t)/cos(t)

Donc tu as cos(t) qui est en dénominateur à 2 reprises sur cette fonction.

Donc quand est-ce que la fonction pourrait admettre une limite (donc ne pas être continue) ?
Quand les dénominateur sont égaux à 0, donc quand cos(t) vaut 0.
Et donc, ta fonction est dérivable sur [0;Pi/2[ si cos(t) n'y est jamais égal à 0, est-ce vrai ?

par **LeJeu** » 02 Nov 2012, 22:21

Vat02 a écrit:tan(t) = sin(t)/cos(t)
Toute fonction continue sur un intervalle est dérivable sur cet intervalle.

Non que non ! je te le disais dans un post précédent

dérivée de f(x) = |x|
en 0 ?

par **Vat02** » 03 Nov 2012, 00:17

LeJeu a écrit:Non que non ! je te le disais dans un post précédent

dérivée de f(x) = |x|
en 0 ?

:mur: Je sais pas ce qui m'est arrivé d'écrire ça à 2 reprises, honte à moi

par **PRC** » 03 Nov 2012, 13:13

Vat02 a écrit:tan(t) = sin(t)/cos(t)

Donc tu as cos(t) qui est en dénominateur à 2 reprises sur cette fonction.

Donc quand est-ce que la fonction pourrait admettre une limite (donc ne pas être continue) ?
Quand les dénominateur sont égaux à 0, donc quand cos(t) vaut 0.
Et donc, ta fonction est dérivable sur [0;Pi/2[ si cos(t) n'y est jamais égal à 0, est-ce vrai ?

Merci Vat02 :we: !
Pour

appartenant à

,

! Donc la fonction est bien dérivable sur cet intervalle.

par **LeJeu** » 03 Nov 2012, 13:26

PRC a écrit:Merci Vat02 :we: !
Pour appartenant à , ! Donc la fonction est bien dérivable sur cet intervalle.

Non, je ne crois pas

Ce n'est pas parceque la fonction est défini que la dérivée existe ! je laisse un forumer plus expert te l'expliquer, mais mon exemple |x| reste valable, la fonction est définie, de plus continue , mais pas dérivable ....

en tous cas le mieux dans le doute ( je ne sais pas mieux) est de calculer la dérivée puis de discuter de son existence

par **Vat02** » 03 Nov 2012, 14:05

LeJeu a écrit:en tous cas le mieux dans le doute ( je ne sais pas mieux) est de calculer la dérivée puis de discuter de son existence

Oui c'est ce que je ferais

Donc PRC ne fais pas attention à ce que j'ai écris c'était une grave erreur.

Dérive ta fonction, et une fois fait tu étudies la continuité de cette dérivée.

par **PRC** » 04 Nov 2012, 14:39

Vat02 a écrit:Oui c'est ce que je ferais

Donc PRC ne fais pas attention à ce que j'ai écris c'était une grave erreur.

Dérive ta fonction, et une fois fait tu étudies la continuité de cette dérivée.

Je ne pense pas qu'il est nécessaire de la dériver car dans mon exercice, on me demande de la dériver à la prochaine question.

Trigonométrie

Trigonométrie

Qui est en ligne