Trigonométrie : limite

par **emdro** » 13 Aoû 2007, 13:07

C'est souvent le même genre de méthodes, en particulier, la mise en facteur "forcée" du plus fort au numérateur, idem au dénominateur, puis la comparaison des plus forts du haut et du bas.

par **lapras** » 13 Aoû 2007, 13:18

Oui effectivement c'est une bonne méthode !

par **J-R** » 13 Aoû 2007, 16:26

je voulais juste toucher un mot de l'Hospitale ....

ma première méthode est plus convenable au lycée....

c'est bon sinon ?

:)

par **emdro** » 13 Aoû 2007, 16:36

Flodelarab a écrit:

àJR: Oui, c'était la bonne idée.

Il faut juste corriger la petite erreur de Flodelarab (le petit 2 à la fin qui s'est perdu):

et on obtient

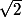
à droite et l'opposé à gauche.

par **lapras** » 13 Aoû 2007, 16:43

C'était bien vu J-R !

par **J-R** » 13 Aoû 2007, 16:49

pas de problème ;)

si tu en veux limites trigo tu me le dis ;)...

par **lapras** » 13 Aoû 2007, 16:50

J'en veux bien s'il te plait ! :we:

par **J-R** » 13 Aoû 2007, 17:00

t'en as là : limites facile

et là lilmite fastoches 2

et là: limite easy 3

par **lapras** » 13 Aoû 2007, 17:06

Ok je vais les faire.

par **lapras** » 13 Aoû 2007, 21:15

merci pour ces trois liens, les limites étaient dans l'ensemble assez simple, mais il y avait de bon conseils de correcteurs. Le plus drole c'es que justement dans le premier lien le théoreme de l'hospital est beaucoup utilisé, malgré le déconseil des correcteurs ^^

par **J-R** » 13 Aoû 2007, 21:19

regarde les méthodes de xunil sans l'hospital elles sont pas mal. De toute facon l'hospitale c'est pour les petits joueurs (je ne l'utilise pas car je ne sais pasle démontrer...)

par **emdro** » 13 Aoû 2007, 21:23

lapras a écrit: le théoreme de l'hospital est beaucoup utilisé, malgré le déconseil des correcteurs ^^

Quel chameau!
C'est parfait de connaître la règle de L'hospital, pour reconnaître d'un coup d'oeil certains cas de forme indéterminée (0/0). Après il reste à présenter avec les taux de variation.

Je me demande si L'hospital n'était pas un méchant personnage, et si ce n'est pas pour cela qu'on hésite à citer son nom... A vérifier.

par **anima** » 13 Aoû 2007, 21:24

emdro a écrit:Je me demande si L'hospital n'était pas un méchant personnage, et si ce n'est pas pour cela qu'on hésite à citer son nom... A vérifier.

Ou peut-etre parce que quand tu entends "regle de l'Hospital" tu penses directement "asile de fous"

L'Hospital est une bonne regle, mais a certains moments seulement. Pareil pour les D.L. et autres conneries du genre, a ne pas utiliser a tout va.

par **lapras** » 13 Aoû 2007, 23:47

Donc si j'ai bien compris, au lieu de citer "d'apres la règle d'hospital", je la démontre en live sur ma copie ?
Apres tout c'est tres simple et tres rapide !
J-R > j'aime bien certaines démonstrations de xunil ! :)
pas mal du tout ce topic que tu m'a présenté !
:++:

par **emdro** » 14 Aoû 2007, 09:14

lapras a écrit:Donc si j'ai bien compris, au lieu de citer "d'apres la règle d'hospital", je la démontre en live sur ma copie ?

C'est exactement ça.

par **lapras** » 14 Aoû 2007, 13:58

Es ce que quelqun aurait des limites trigonométriques niveau premiere S vraiment bien compliquées ?

merci d'avance

par **J-R** » 14 Aoû 2007, 19:35

en limite trigo on ne peut pas trouver plus difficille ( a ce que j'ai fait jusq' maintenant). C'est toujours pareil: on transforme l'expression en une autre à l'aide d'un taux de variation, des formules trigo, des limites déja connues....

par **lapras** » 14 Aoû 2007, 19:56

Mince, :( J'adorais les limites trigonométriques
Il y'en a des plus durs en terminale S ?

par **emdro** » 14 Aoû 2007, 19:59

NON! :happy2:

par **Skullkid** » 14 Aoû 2007, 20:00

Faudra attendre le post-bac je pense ^^

(sauf si t'apprends les méthodes par toi-même avant, ce qui est fort possible !)

Trigonométrie : limite

Qui est en ligne