Triangle direct dans un repère : suites DM

[Anonyme]

Bonjour, j'ai un exercice à résoudre et j'aurais besoin d'aide pour me corriger ce j'ai déjà fait et ce que je n'ai pas encore fait :S

voici la figure :



Mes QUESTIONS/REPONSES :

1°) Calculer 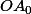; 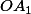et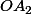

--> donc

--> D'après le triangle , rectangle isocèle direct en , on a :








--> donc


2°) Exprimer en fonction de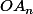
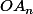
Pour exprimer en fonction de , on utilise le théorème de pythagore.
D'après le triangle , rectangle isocèle en , on a :





mon problème c'est que à partir de là je bloque totalement ! pourriez-vous me donner des indications svp ?


3°) an = OAn. Déduire la nature de la suite (an)
4°) Déterminez l'expression de an en fonction de n, avec n entier naturel

Pour les questions 3°) et 4°) je peux pas les faire si je n'ai pas répondu à la question 2 :/

Merci d'avance pour l'aide

[Ericovitchi]

Bonjour, donc tu as démontré que donc
Ça c'est de la forme , ça devrait t'inspirer ?

[Anonyme]

Bonjour, donc tu as démontré que donc
Ça c'est de la forme , ça devrait t'inspirer ?

Comment est-ce qu'on passe de à ? :S

Oui cette forme signifie que c'est une suite géométrique de raison

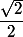
[Kikoo <3 Bieber]

Comment est-ce qu'on passe de à ? :S

Oui cette forme signifie que c'est une suite géométrique de raison

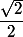
Hello,

Quand on rabaisse à la racine (en prenant des valeurs positives car on parle de distances), eh ben on a 1/sqrt{2} qui vaut sqrt{2}/2

[Anonyme]

Hello,

Quand on rabaisse à la racine (en prenant des valeurs positives car on parle de distances), eh ben on a 1/sqrt{2} qui vaut sqrt{2}/2

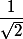
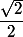
La racine carré se porte sur pas sur . Ce que je ne comprends pas c'est comment on passe de à ? On multiplie par alors ?

[Ericovitchi]

[Anonyme]

Pour information :



Exercice :
Simplifier l'expression suivante

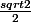ps)
Question bonus :
expliquer pourquoi ?

[Anonyme]

Mon dieu honte à moi ! j'avais complètement oublier que il faut donc bien multiplier par


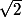3°) an = OAn. Déduire la nature de la suite (an)

La suite (an) est une suite géométrique de raison

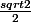4°) Déterminez l'expression de an en fonction de n, avec n entier naturel

an =

Est-ce juste ?

[Ericovitchi]

Attention a0=2

[Kikoo <3 Bieber]

Question bonus :
expliquer pourquoi ?

On passe par la structure de (Z,+,.) par exemple :

L'unique neutre par la multiplication est 1 blablabla...

PS : il se peut que j'aie dit des bêtises. est l'unique réel dont le carré vaut x (car application bijective). Et ça suffit non ?

[Anonyme]

Attention a0=2

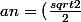a0 = 2 ? ça veut dire que n'est pas correct alors parce que sinon j'ai a0 = 1/1 = 1 :s

[Kikoo <3 Bieber]

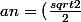a0 = 2 ? ça veut dire que n'est pas correct alors parce que sinon j'ai a0 = 1/1 = 1 :s

Oui, il est passé où le premier terme ?

[Anonyme]

Oui, il est passé où le premier terme ?

comment ça il est passé où le premier terme ? c'est a0 le premier terme :/

[Kikoo <3 Bieber]

comment ça il est passé où le premier terme ? c'est a0 le premier terme :/

Oui, mais je ne le vois pas dans l'expression de ... Il faut que tu revoies ton cours. Il y est très clairement indiqué l'expression générale d'une suite géométrique.

[Anonyme]

mais y'a un problème parce que quoi qu'il arrive a0 = 1 car tout nombre à la puissance 0 donne 1 :S

[Anonyme]

Oui, mais je ne le vois pas dans l'expression de ... Il faut que tu revoies ton cours. Il y est très clairement indiqué l'expression générale d'une suite géométrique.

ah oui oui vous avez raison !

[Kikoo <3 Bieber]

mais y'a un problème parce que quoi qu'il arrive a0 = 1 car tout nombre à la puissance 0 donne 1 :S

Oui, ben il te manque effectivement quelque chose pour que cela soit juste. Go look cours :book:

[Anonyme]

mais comment on sait que a0 = 2 ?

pour la suite géométrique l'expression est

[Kikoo <3 Bieber]

Parce que c'est donné dans ton énoncé : est la suite qui à chaque i de {0,...,n} donne la distance de O à un certain sommet de ta figure.

Le premier terme, , est la longueur .

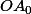
[Anonyme]

Parce que c'est donné par ton énoncé : est la suite qui à chaque i de {0,...,n} donne la distance de O à un certain sommet de ta figure.

Le premier terme, , est la longueur .

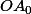
aaaaah ouaaaais !! donc en gros j'ai